Задания 1-го тура XVI олимпиады по математике для 4 класса

Чему равна сторона равностороннего треугольника, который сложили из треугольников с равными сторонами А, В и С и периметром 3 см, если было использовано 36 треугольников?

На велосипедной трассе от линии старта до линии финиша на равном расстоянии установлены столбы. Через 20 минут велосипедист был около 5 столба. Через сколько минут от начала гонки велосипедист будет у 9 столба? Будем считать, что скорость велосипедиста постоянна.

В магазин привезли валенки: серого, бежевого и черного цветов разных размеров: 36, 38, 40. Все в одной коробке, причём есть по 3 пары валенок каждого из возможных сочетаний цвета и размера. Продавщица не успела разобрать коробку по парам, когда в магазин зашла бабушка и попросила померить черные валенки 36 размера. Валенки несимметричные: валенки на правую и на левую ногу — разные. Какое минимальное количество валенок должна будет достать продавщица из коробки не глядя, чтобы точно достать нужную пару?

В пещере гнома очень темно. Чтобы пройти по тоннелю, гном взял с собой свечи. Гном зажёг первую свечку, а вторую свечку он зажег после того, как первая прогорела на две третьих. Третью свечку он зажег после того, как вторая прогорела на две трети. Сколько времени гном будет идти по тоннелю с двумя одновременно горящими свечами, если каждая свечка полностью сгорает за 1 час 30 минут?

У Мухи-Цокотухи множество дочерей и сыновей. Однажды, она открыла коробку конфет и разрешила всем мушатам взять по 3 конфетки. От сладкого у детишек заболели животы, поэтому, на следующий день, когда она открыла такую же коробку конфет, она разрешила всем брать только по одной конфетке. Сколько детей у Цокотухи, если в первый день в коробке осталось всего одна конфета, а во второй – 31?

Первый звонок звонит каждые 6 минут. Второй звонок звонит каждые 7 минут. Третий звонок звонит каждый час. Если в полдень все колокола зазвонят одновременно, в какое время они в следующий раз зазвонят одновременно?

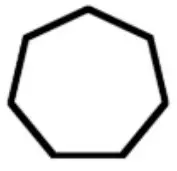
Возле каждой стены в семиугольной комнате поставили по 3 стула. Сколько стульев оказалось в углах, если всего их было 17?

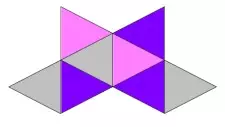
Сосчитайте сколько четырёхугольников в этой фигуре?

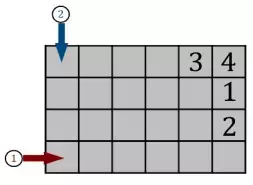
Двое рабочих укладывают плитку. Первый: • выкладывает слева направо, начиная с нижнего ряда; • когда один ряд закончен, рабочий переходит на ряд выше, сохраняя направление работы. Второй: • выкладывает плитку сверху вниз, начиная с крайнего левого ряда; • когда один ряд закончен, рабочий переходит на ряд правее, сохраняя направление работы. Если плитка уже положена, то второй раз её не укладывают. Начинают они одновременно, работают с одинаковой скоростью. Какую плитку первый рабочий уложит последней?

Семья циркачей несколько дней подряд исполняет номер «Башенка». Для этого члены семейства встают на плечи друг к другу в один или несколько рядов так, чтобы в любом ряду ниже было не меньше человек, чем в ряду выше. Сколько дней подряд циркачи могут составлять «Башенки» из 6 человек, не повторяясь, если в «Башенке» должен быть хотя бы один ряд?