Задания 2-го тура XV олимпиады по математике для 4 класса
2 тур XV олимпиады по математике прошел 25 февраля 2024 года.
Задачи олимпиады
Задача №1
Сосчитайте сколько ромбов в этой фигуре?
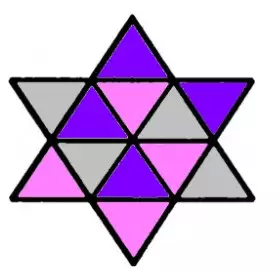
Иванюк Е. В.
Задача №2
На доске написано число 32. Двое по очереди выписывают на доску следующее число, полученное вычитанием из предыдущего его остатка от деления на 5, 11 или 13. Проиграет тот, кто получит 0. Кто победит при правильной игре, если два одинаковых числа подряд выписывать на доску запрещено?
Галиулина В. Н.
Задача №3
Можно ли расставить простые числа в кружочки так, чтобы разность никаких двух соседних не делилась на 3? (Простыми числами называются те числа, которые делятся только сами на себя и на 1.)

Галиулина В. Н.
Задача №4
Вокруг большой лужи встали 20 жителей острова рыцарей и лжецов и посмотрели на неё. Потом каждый из 20 людей грустно сказал: «Среди следующих трёх людей справа от меня по кругу есть хотя бы 2 рыцаря». Сколько среди них было рыцарей? (Рыцари всегда говорят правду, лжецы всегда лгут)
Галиулина В. Н.
Задача №5
Если справа от суммы цифр двузначного числа N приписать произведение его цифр, то результат будет равняться исходному числу N. Найдите все такие числа и докажите, что других нет.
Галиулина В. Н.
Задача №6
Расшифруйте пример на умножение (т. е. вместо звездочек нужно поставить цифры, возможно одинаковые, так, чтобы получилось верное равенство).
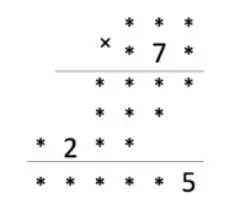
Галиулина В. Н.
Задача №7
Элемент может быть прикреплен к электросхеме четырьмя способами: Если медные проводки двух элементов соприкасаются, случается короткое замыкание (см. картинку) Докажите, что нельзя заполнить элементами всю схему так, чтобы не случилось короткого замыкания.
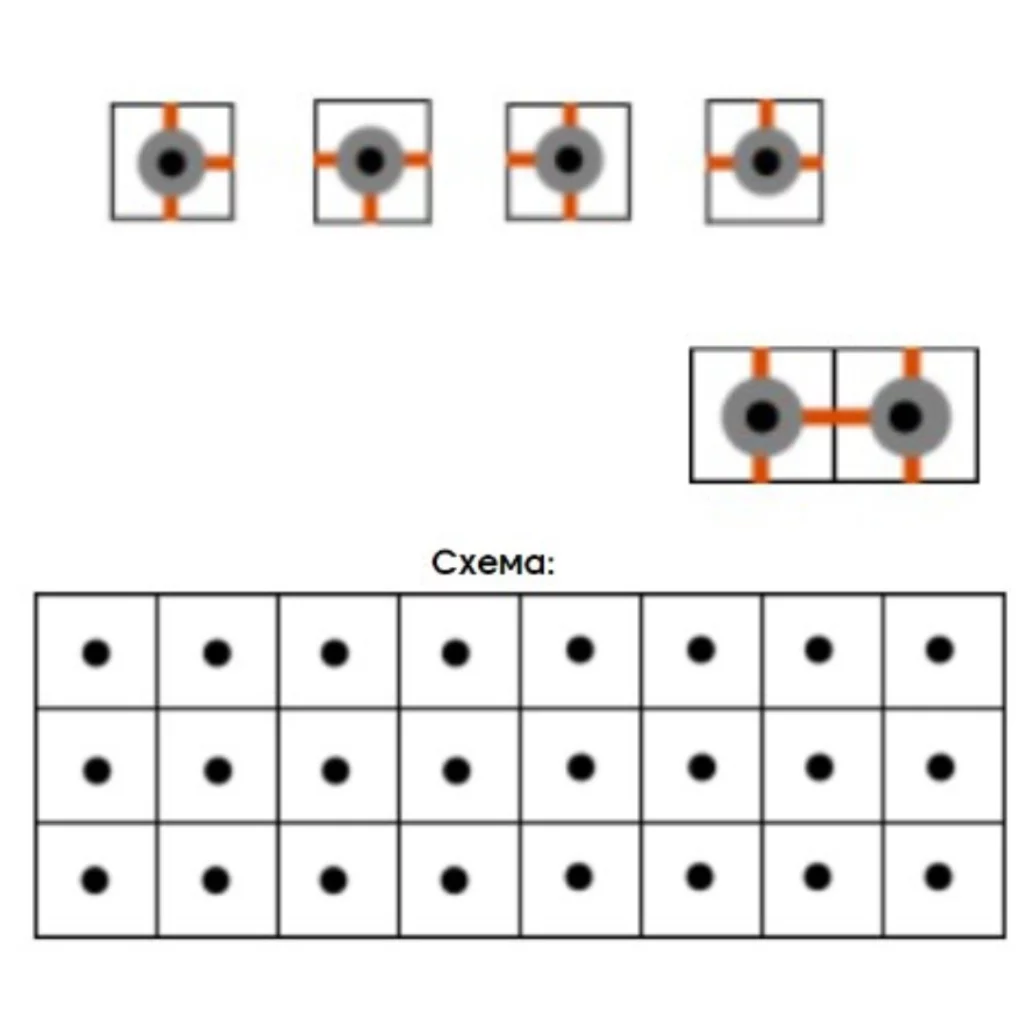
Галиулина В. Н.
Задача №8
На доске написано 100 попарно различных натуральных чисел, каждое из которых не превышает 1000. В мешочке лежат 1200 карточек со знаком «-» и 250 карточек со знаком «+». Каждый ход Вася наугад достает карточку из мешочка. Если попался минус, то из каждого числа он вычитает 1. Если попался плюс, то к каждому числу он прибавляет 1. Докажите, что в какой-то момент ровно половина чисел окажутся положительными.
Галиулина В. Н.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


