Задания 1-го тура XV олимпиады по математике для 4 класса
1 тур XV олимпиады по математике прошел с 15 января по 6 февраля 2024 года.
Задачи олимпиады
Задача №1
По дороге в магазин Маша прошла мимо дома Сережи. Из магазина она пошла в гости к Свете, попутно пройдя мимо своего дома. Где живет Света?
(А) в фиолетовом домике (Б) в жёлтом домике (В) в красном домике (Г) в зелёном домике (Д) в оранжевом домике
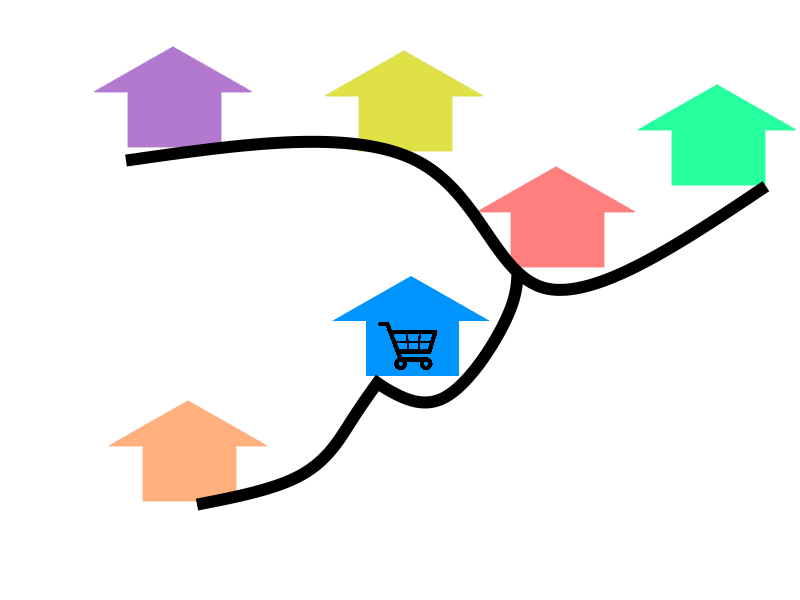
Галиулина В. Н.
Задача №2
В четыре пробирки налита кислота. Высота каждой пробирки – 12 см. 1-й и 2-й стакан заполнены до отметки в 9 см, 3-й – до отметки в 10 см, 4-й – до отметки в 4 см. Грю хочет разлить кислоту так, чтобы во всех пробирках ее оказалось поровну. За один раз он может перелить кислоту из одной пробирки в другую так, чтобы вторая оказалась заполнена до краев, либо так, кислоты в пробирках стало поровну. За какое наименьшее количество шагов он может это сделать?
(А) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5

Галиулина В. Н.
Задача №3
На паутине висело несколько существ - жуков и пауков. Чтобы раскрыть очень запутанное дело, Жак Клузо пересчитал головы и лапки всех существ. Оказалось, что лапок было 82, а голов 12. Помогите непревзойденному детективу раскрыть дело – выяснить сколько на паутине висело жуков.
(А) 4 (Б) 6 (В) 7 (Г) 8
Галиулина В. Н.
Задача №4
Некоторые кочки на болоте в лягушачьей деревне соединены мостиками, как показано на рисунке, лягушонок Прутик может На сколько одинаковых фигурок можно разрезать фигурку нарисованную ниже. Части не могут состоять из 1 плиточки.
(А) 21 (Б) 10 (В) 3 (Г) 7 (Д) разрезать нельзя
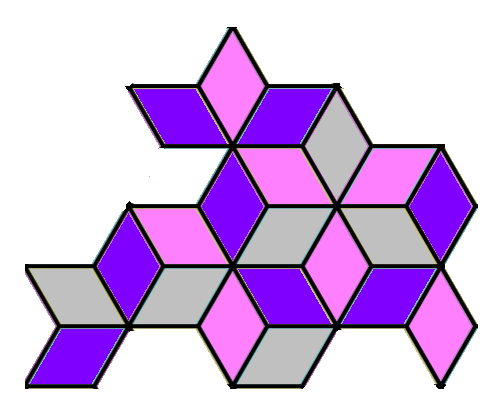
Задача №5
Фрекен Бок подарила Малышу шоколадку, разделённую бороздками на 6 × 8 маленьких плиточек. Карлсон предлагает Малышу сыграть в такую игру. Каждый по очереди разламывает любой из кусков по одной из бороздок (по прямой от края до края). Тот, после хода которого вся шоколадка будет разделена на отдельные плиточки, съедает всю шоколадку. Чтобы сходить первому, Карлсон предлагает делить шоколадку в следующей последовательности: Карлсон, Малыш, Фрекен Бок, Малыш, Карлсон, Малыш, Фрекен Бок, Малыш и т.д. Кто выиграет и съест шоколадку?
(А) Карлсон (Б) Малыш (В) Фрекен Бок (Г) невозможно определить
Иванюк Е. В.
Задача №6
Дядя Фёдор выкладывал из палочек римские числа по порядку от 1 до 11, причём чтобы выложить I ему нужна одна спичка, а чтобы выложить V и X -- по две. Пришёл Шарик и убрал слева и справа по 14 палочек. Какое число осталось у Дяди Фёдора?
(А) IV (Б) V (В) VI (Г) VII (Д) VIII
Иванюк Е. В.
Задача №7
С утра многоножка решила отправиться на прогулку. На то, чтобы надеть обувь на каждую из первых двадцати пар ног у нее ушло 40 минут. Вечером многоножка начала разуваться. Когда прошло 20 минут, она, устало вздохнув, взглянула на свои ноги и увидела, что осталось еще целых десять пар. Сколько ног у многоножки, если разувается она в два раза быстрей, чем обувается?
(А) 30 (Б) 40 (В) 50 (Г) 60 (Д) 80
Галиулина В. Н.
Задача №8
Среди учеников 4-го «М» класса каждый был либо на экскурсии, либо в театре, либо в походе. Все, кто был в театре, после спектакля пошли на экскурсию. Тех, кто не был в походе, меньше, чем тех, кто не был на экскурсии. На каком мероприятии было больше всего детей?
(А) на экскурсии (Б) в театре (В) в походе (Г) невозможно определить
Галиулина В. Н.
Задача №9
Таня перечитывала свой старый дневник и наткнулась на запись: «Ровно неделю назад Даня сказал мне, что позавчера Лена ему сказала, что через три дня у нее будет День Рождения. Ей исполнилось 8 лет». Когда была сделана запись, если Таня помнит, что у Лена родилась 29 декабря 2013 года?
(А) 4 января 2021 года (Б) 31 декабря 2021 года (В) 6 января 2022 года (Г) 4 января 2022 года (Д) 6 января 2021 года
Галиулина В. Н.
Задача №10
Сколько ниточек между алмазами нужно разрезать, чтобы большое алмазное колье с картинки превратилось в алмазную нить, если все бусины из колье должны оказаться нанизанными на нить? Например, в колье из четырех бусин пришлось бы отрезать всего одну ниточку, как показано ниже.
(А) 8 (Б) 9 (В) 10 (Г) 11 (Д) 12
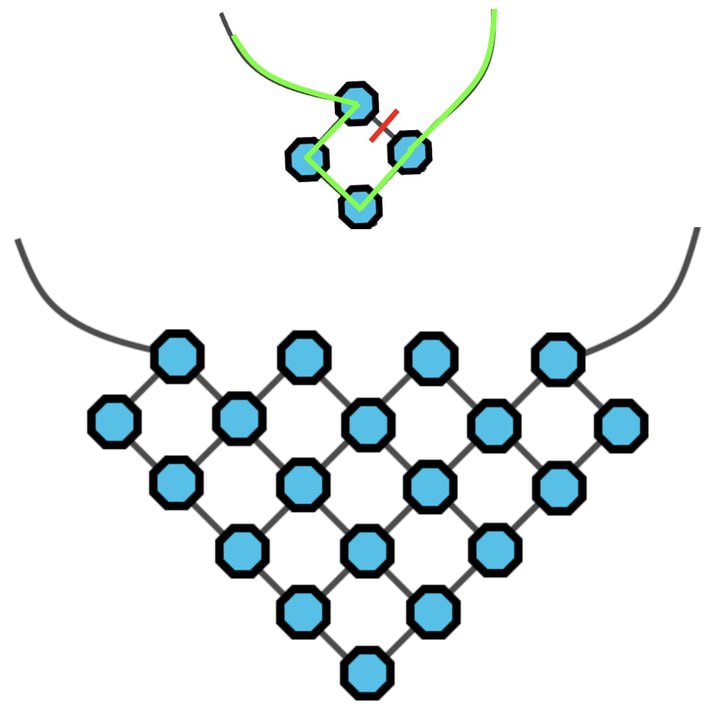
Галиулина В. Н.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | А | В | В | В | В | В | Г | В | Г | B |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


