Задания 1-го тура XVIII олимпиады по математике для 7 класса

В магазине, который закупает одинаковые кроссовки у поставщика оптом и продает их в розницу, идет акция: при покупке двух пар обуви — скидка 10%, а при покупке трех пар — скидка 20% на эту покупку. Какая наценка у магазина в процентах (на сколько процентов розничная цена больше закупочной), если магазин имеет одинаковую прибыль с каждой продажи со скидкой. Ответ дайте в процентах, округлив до ближайшего целого.

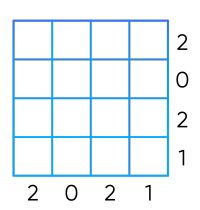
В сетке 4×4 некоторые ячейки должны быть окрашены в черный цвет. Цифры справа от сетки и под ней показывают, сколько ячеек в этой строке или столбце должны быть черными. Сколькими способами можно раскрасить эту сетку?

У Васи было поровну четырехугольников и треугольников. Каждый четырехугольник он разрезал на 2 треугольника, а каждый треугольник — на треугольник и четырехугольник. А затем снова сделал тоже самое с новыми фигурками. В итоге у него получилось 50 треугольников. А сколько получилось четырехугольников?

На картинке все самые маленькие треугольнички правильные и их площадь равна 1. Чему равна площадь всей фигуры?

На доске написано число 12. Петя и Вика по очереди приписывают к числу на доске справа четную цифру. Начинает Петя. Петя хочет, чтобы после каждого его хода число делилось на n. При каком наибольшем из перечисленных n он сможет этого добиться, вне зависимости от действий Вики?

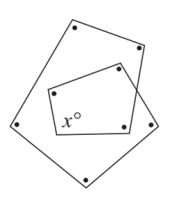
На рисунке все отмеченные углы точкой равны углу, обозначенному как x°. Чему равен x ?

Петя выложил в ряд девять коробок. В двух из них лежат синие шарики, в трёх — красные и ещё в четырёх — зелёные. Он помнит, что цвета шариков в соседних коробках различаются и что во второй и шестой коробках шарики красные, а в восьмой — не зелёный, а в первой — синий. Сколько коробок ему нужно открыть, чтобы гарантированно понять, где лежат все три красных шарика?

На доске было написано неверное равенство 1+2+3+…+20 = 21+22+23+…+40 (с каждой стороны по 20 слагаемых). Какое наименьшее количество плюсов нужно заменить на минусы, чтобы равенство стало верным? (Скобки использовать нельзя)

Сколько существует пар натуральных чисел n n, m m таких, что n + ( n + 1 ) + ( n + 2 ) + … + ( n + m ) = 1000 n+(n+1)+(n+2)+…+(n+m)=1000?

Сколько дробей вида a/b удовлетворяет всем условиям ниже: - числа a и b целые; - дробь a/b несократима; - её значение отрицательно; если к числителю прибавить 18, а к знаменателю 15, то значение дроби увеличится в 10 раз?