Задания Тринадцатой Олимпиады по математике Весна 2023 1 тур 7 класс

1 тур олимпиады по математике прошёл с 15 мая по 7 июня 2023 года

Задача №1
Пока папы не было дома Петя и Лёша начали скачивать на домашний сервер игры. Чтобы найти и скачать 10 игр, Пете требуется 36 минут, а Лёше — 45 минут. Папа по удалённому соединению, обнаруживает и удаляет 10 игр за час. Всё это делается одновременно. Когда папа впервые увидел 12 скачанных и не удалённых игр он отключил домашний сервер. Сколько времени дети скачивали игры?
(А) 30 минут
(Б) 36 минут
(В) 42 минуты
(Г) 48 минут
(Д) 54 минуты

Задача №2
Из куба 3х3х3 вырезали несколько кубиков как показано на рисунке.
Как изменилась площадь поверхности? (вырез в виде буквы П перевернутой вниз и сверху удалены ещё несколько кубиков)

(А) Увеличилась на 9
(Б) Увеличилась на 8
(В) Увеличилась на 7
(Г) Уменьшилась на 7
(Д) Не изменилась

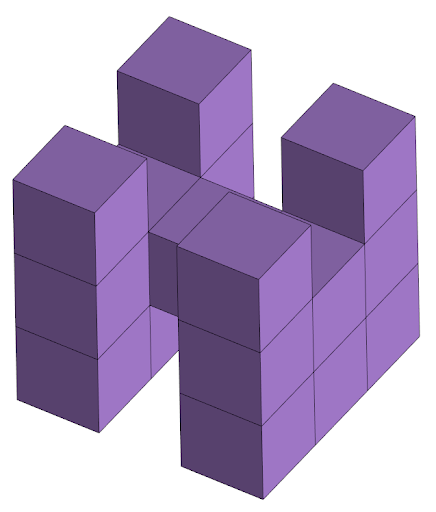
Задача №3
Машенька вырезала из квадратного листочка в клеточку квадрат меньшего размера, ровно по границам клеточек. Какого максимального размера мог быть первоначальный квадрат если остался кусочек площадью в 2021 клеточку. Введите число — сторону первоначального квадрата.

Задача №4
Сколько решений есть у уравнения:

(А) 0
(Б) 5
(В) 3
(Г) 7
(Д) 9

Задача №5
У могучего чародея Арчибальда Вольдемаровича есть большая коллекция магических испаряющихся шариков. Если черный шар положить справа от белого, то они притянутся друг к другу, столкнутся и испарятся. Если слева, то они просто притянутся друг к другу и останутся лежать. Волшебник разложил их в таком порядке: один белый, два черных, три белых, четыре черных. И так далее. Цепочку замыкают 100 черных шариков. Сколько шаров останется после того, как все, которые могут, испарятся?
(А) 4950
(Б) 150
(В) 100
(Г) 50
(Д) 0

Задача №6
У вас есть набор палочек, лежащих в виде сетки. Вы забираете палочки по одной начиная с самого верха. Чему будет равно значение полученного выражения? Пожалуйста, не забывайте про порядок действий. В ответ введите число.

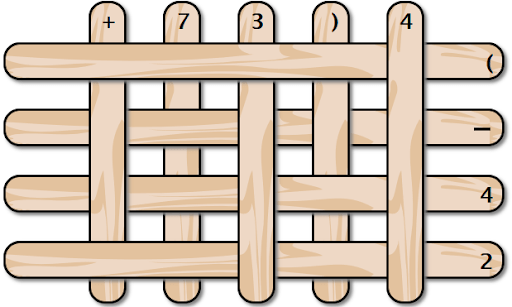
Задача №7
Расставьте в выражении цифры от 1 до 9 так чтобы получилось верное равенство.
Чему равно центральное число если точно известно, что в нём нет 7?

Задача №8
Сколько прямоугольников в фигуре на картинке?

(А) 16
(Б) 40
(В) 84
(Г) 100
(Д) 256

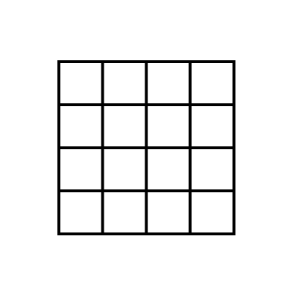
Задача №9
Бельчонок Натти просто обожает сладости. Он купил в лавке несколько бутылок вишневого сиропа и, недолго думая, выпил их все.
В той же лавке можно обменять некоторое количество (одно и то же) пустых бутылок на целую бутылку сиропа. Бельчонок возвращался в лавку несколько раз чтобы обменять бутылки, и, путем обмена он получил еще 6 бутылок сиропа. В конечном итоге, у него осталось 5 пустых бутылок. А если бы он купил в два раза больше сиропа, то ему пришлось бы обменивать бутылки 13 раз, и, в результате, у него бы осталось 3 пустых бутылки. Сколько пустых бутылок можно обменять на полную?
(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 11

Задача №10
Художник Тюбик захотел нарисовать одинаковое количество синих, зеленых и желтых одинаковых кружочков. Сначала он нарисовал синие и желтые круги. У него были только синяя и желтая краска, однако, художник не унывал, ведь если нарисовать синий кружок поверх желтого, то получится зеленый. В какой-то момент у него закончилась синяя краска, и он заказал ее на OnlyExpress. Однако, краска оказалась бракованная, и она просто перекрашивала желтые кружки в синий цвет. В результате, синих кружков оказалось вдвое больше зеленых. Во сколько раз у Тюбика было больше хорошей синей краски чем плохой, если к концу работы новая краска тоже закончилась?
(А) 0,5
(Б) 2
(В) 3
(Г) 5
(Д) Невозможно определить