Задания 1-го тура XIV олимпиады по математике для 7 класса

Сколько существует нечетных трехзначных чисел с произведением цифр 18? (А) 6 (Б) 9 (В) 8 (Г) 10 (Д) 12

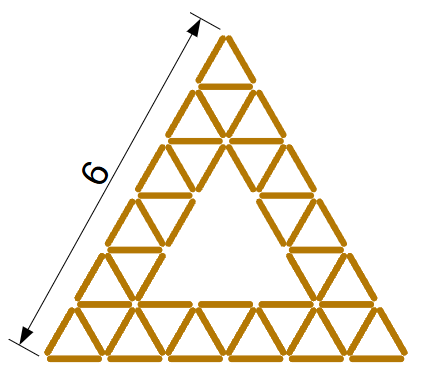
Лёша складывает из спичек треугольник по образцу (см. рис). Сколько спичек придётся потратить на фигуру со стороной равной 12? (А) 123 (Б) 126 (В) 129 (Г) 132 (Д) 135

Найти наибольшее a, для которого существует положительное b, такое, что (А) 0 (Б) 4 (В) 6 (Г) 9 (Д) 10

Двигатель ледокола расходует уголь. Есть два вида контейнеров с углем - маленькие и большие. Известно, что большой контейнер с углем вмещает в себя столько же угля, сколько целое количество маленьких. Для десятидневного путешествия необходимо три маленьких и три больших контейнера угля, а для шестидневного - 1 большой и 14 маленьких. На ледокол загружают минимальное возможное количество контейнеров угля так, чтобы суммарный вес угля тоже был минимальным, но не гарантировано, что последний контейнер будет израсходован полностью. Сколько маленьких контейнеров содержат столько же угля, сколько один большой? (А) 15 (Б) 16 (В) 18 (Г) 24 (Д) нет однозначного ответа

У Таи есть два прямоугольника с целыми длинами сторон. Она заметила, что площадь первого численно равна периметру второго, а площадь второго численно равна периметру первого. Площадь одного из прямоугольников равна 54. Чему может быть равна площадь второго? (А) 182 (Б) 110 (В) 121 (Г) 108

Софья Васильевна больше всего в жизни любит математику, своих внуков и печь пирожки. Однажды к ней приехали её внучата, и чтобы побаловать их, она решила испечь много-много пирожков и сложить их на большой поднос. Наблюдательная Софья Васильевна заметила, что если каждый внук возьмёт по одному пирожку, то на подносе их останется 49, а если бы каждый внук, наоборот, положил по одному пирожку на поднос, то их стало бы 63. Сколько пирожков достанется каждому внуку, если они поровну разделят пирожки между собой? (А) 6 (Б) 7 (В) 8 (Г) 9

Матвей выписал в порядке возрастания все пятизначные числа, состоящие из цифр 1, 2, 3, 4, и 5, взятых по одному разу. На каком месте оказалось число 32451? (А) 24 (Б) 56 (В) 58 (Г) 63

На одной чаше весов лежит гирька весом 23 грамма. У Кати есть набор гирек весом 1, 2, 3, 4, 5, ... грамм. Катя достаёт гирьки в порядке увеличения веса и кладёт их на какую-то из чаш. Какое минимальное количество гирек должна достать Катя, чтобы чаши пришли в равновесие? (А) 6 (Б) 7 (В) 8 (Г) 9

На фабрике произвели по 120 перчаток трех разных размеров. И правых, и левых всех размеров - по 180 штук. Какое максимальное количество нормальных пар перчаток гарантированно можно составить из этих 360? В нормальной паре есть как левая, так и правая перчатка и их размеры одинаковы. Все левые, и все правые перчатки одного размера одинаковы. (А) 30 (Б) 60 (В) 90 (Г) 120 (Д) 240

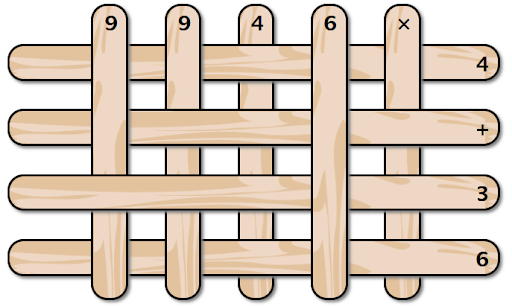
У вас есть набор палочек лежащих в виде сетки. Вы забираете палочки по одной начиная с самого верха. Чему будет равно значение полученное выражение? Пожалуйста, не забывайте про порядок действий. В ответ введите число.