Задания математической олимпиады 3-4 класс

На данной страницы размещены олимпиадные задания с решением для 1 класса.
Олимпиада по математике прошла 1 октября 2017 года

Cкачать задание в формате Pdf

Посмотреть ответы на все задания олимпиады

Олимпиада «Праздник Математики», 01.10.2017

Задача №1

Разделите фигуру по линиям сторон шестиугольников на три равные по форме и размеру части.

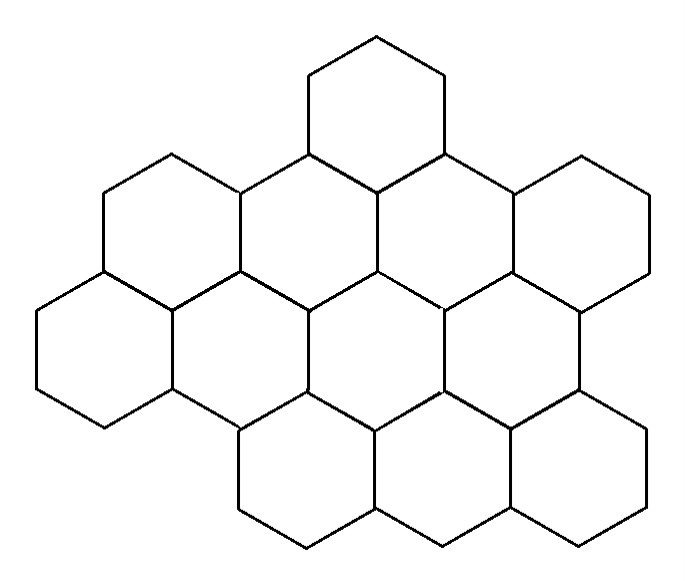
Задача №2

В подарочном мешке лежат красные и жёлтые штуковины. Некоторые из них квадратные, остальные круглые. Марина Валерьевна достает из мешка штуковину и показывает её всему классу. Ваня говорит: «Это штуковина красная или квадратная». Женя говорит: «Если она жёлтая, то она квадратная». В этом классе девочки говорят правду, а мальчики врут. Какая по форме и цвету штуковина? Женя мальчик или девочка? Ответ подробно объясните.

Задача №3

В классе у каждого из 20 человек есть смартфон или спиннер. Владельцев спиннеров на 7 больше чем обладателей смартфонов. Докажите, что хотя бы у одного человека есть и спиннер, и смартфон.

Задача №4

На фестиваль «Кони и Люди» зарегистрировалось некоторое количество участников — коней и людей. Далее в связи с уборкой урожая от участия отказалась треть зарегистрировавшихся, из-за чего общее количество ног уменьшилось в два раза. Пришёл ли хотя бы один конь на фестиваль? Ответ объясните.

Задача №5

В каждой клетке доски 6х6 клеток сидит хомяк. Ровно в полночь каждый хомяк переползает через одну клетку по вертикали или горизонтали. Может ли оказаться, что после этого переползания в каждой клетке сидит ровно один хомяк? Если может, показать, как хомяки ползли. Если не может, объяснить почему.

Задача №6

На поле 6х6 клеток спрятался четырёхпалубный корабль (4 клетки подряд в строку или столбец). Можно ли сделать 8 выстрелов так, чтобы точно попасть в этот корабль? Если можно, показать, куда стрелять. Если нельзя, то объяснить, почему.

Задача №7

В каждом подъезде одинаковое число этажей (больше одного), на каждом этаже одинаковое число квартир (больше одной). Квартиры 15 и 31 не в одном подъезде и не в соседних подъездах. Квартиры 45 и 46 не на одном этаже и не на соседних этажах. В каком подъезде и на каком этаже 28 квартира? Ответ объясните.

Задача №8

Ученики 3 класса на первый урок физкультуры выстроились в ряд, чередуясь мальчик — девочка. Среди любых 10 человек класса обязательно найдется хотя бы одна девочка. Сколько девочек может быть в классе? Найдите все ответы и объясните почему нет других