Задания Четвертой Олимпиады по математике Зима 2019 3 класс

На данной страницы размещены олимпиадные задания с решением для 3 класса.
Олимпиада по математике прошла 27 января 2019 года

Cкачать задание в формате Pdf

Посмотреть ответы на все задания олимпиады

Задание IV Олимпиады по математике 3 класс

Задача № 1

Разделите фигуру на 6 равных частей.

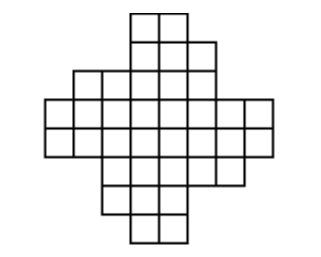
Задача № 2

Поверхность октаэдра состоит из 8 равносторонних треугольников. Будем две грани октаэдра называть противоположными, если они не имеют общих точек. Грани октаэдра пронумеровали числами от 1 до 8 так, что сумма чисел на противоположных гранях равна 9. Расставьте на развертке октаэдра оставшиеся числа.

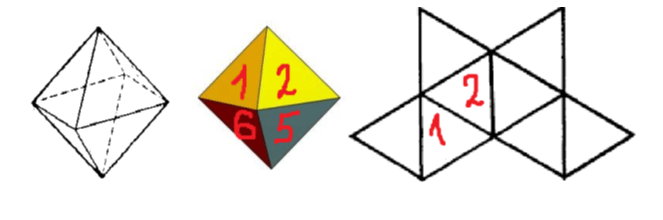
Задача № 3

Ширина ковровой дорожки 1 метр. На сколько метров пунктирный (черно-серый) контур длиннее чем сплошной (черный)?

Задача № 4

Ника рисовала кружочки. Каждый раз у неё получалась фигура, похожая на шестиугольник. Сколько кружочков будет в таком шестиугольнике, если на одной стороне будет 10 кружочков?

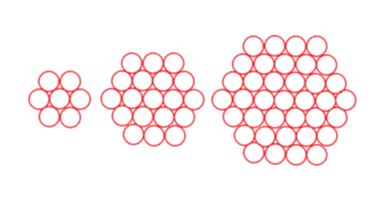
Задача № 5

Какое наибольшее количество ферзей можно поставить на доску 8х8 так, чтобы они не били друг друга. Нарисуйте схему и объясните, почему нельзя расставить больше.

Задача № 6

Какое наименьшее количество прямоугольников 1х3 нужно закрасить на поле 12х12, чтобы в любом квадрате 4х4 была хотя бы одна окрашенная клетка. Закрасьте прямоугольники, и объясните, почему нельзя закрасить меньше.

Все материалы математических олимпиад для 3 класса

Задания, ответы и разборы, списки победителей

Другие задания олимпиад по математике для 3-х классов

Осень 2017 — Математическая олимпиада, 3 класс
Зима 2018 — Математическая олимпиада, 3 класс
Осень 2018 — Математическая олимпиада, 3 класс
Зима 2019 — Математическая олимпиада, 3 класс
Осень 2019 — Математическая олимпиада, 3 класс
Зима 2020 — Математическая олимпиада, 3 класс

Все материалы математических олимпиад за 2019 год

Задачи, ответы и разборы, списки победителей