Задания Тринадцатой Олимпиады по математике Весна 2023 1 тур 3 класс

1 тур олимпиады по математике прошёл с 15 мая по 7 июня 2023 года

Задача №1
На столе лежат 5 коробочек. В каждую коробочку кладут не меньше 1 и не больше 5 пуговиц. В каждой коробочке разное количество пуговиц. Сколько всего пуговиц во всех коробочках?
(A) 12
(Б) 15
(В) 18
(Г) 20
(Д) 21

Задача №2
Три друга собирали грибы. Вечером, когда они решили подсчитать, кто сколько собрал, оказалось, что Петя собрал в 2 раза больше Кости, а Дима собрал на 1 гриб меньше Пети. Всего они собрали 24 гриба. Сколько грибов собрал Дима?
(A) 5
(Б) 6
(В) 8
(Г) 9
(Д) 10

Задача №3
На скамейке сидят Ваня, его папа, дедушка и кот. Дедушка не сидит рядом с котом. Внук сел рядом с дедушкой. Папа не сидит рядом с котом. Кто сидит рядом с папой?
(A) Ваня
(Б) Дедушка
(В) Ваня и дедушка
(Г) Ваня и кот
(Д) Дедушка и кот

Задача №4
Машина едет по проселочной дороге со скоростью 20 метров за 2 секунды, а по шоссе вдвое быстрее. Какое расстояние проедет машина за час по шоссе?
(А) 36 км
(Б) 4800 м
(В) 60 км
(Г) 72 км
(Д) 9600 м

Задача №5
Три богатыря Илья, Алеша и Добрыня решили выяснить, кто из них самый быстрый. На полосе препятствий пока Илья делает 6 шага, Алеша – 10 шагов. Пока Алеша делает 6 шагов, Добрыня — 10 шагов. Юлий посчитал, что Алеша и Добрыня вместе сделали 800 шагов. Сколько шагов сделал Илья?
(A) 150
(Б) 300
(В) 180
(Г) 240

Задача №6
У Коржика 5 шариков, а у Карамельки — меньше шариков, чем у Коржика, у Компота столько же шариков, сколько у Коржика и Карамельки вместе. Сколько может быть всего шариков у трех котят?
(A) 11
(Б) 13
(В) 14
(Г) 20

Задача №7
Числа от 1 до 10 расставлены в кругах так, что сумма в каждом круге одинаковая. Цифры 1,2,3,4,5,6,7 могут находиться в нескольких кругах
одновременно. Чему равна сумма чисел в круге?

(A) 28
(Б) 26
(В) 32
(Г) 24
(Д) 25

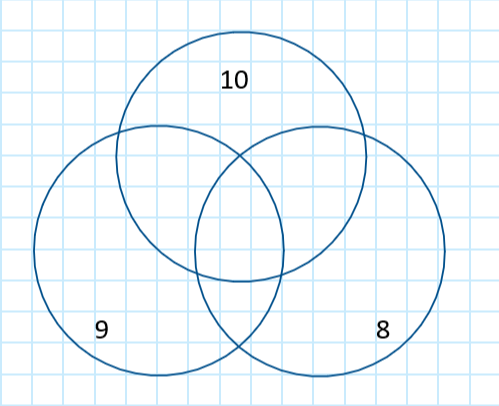
Задача №8
Таня, Аня, Галя и Валя участвовали в соревновании по сбору ягод на скорость. После окончания соревнования, девочки выстроили ведра с ягодами в ряд от самого полного к самому пустому. Известно, что никто из девочек не собрал одинаковое количество ягод, Валя набрала ягод больше, чем Таня и Аня вместе взятые, а ведерко Гали стояло между Аниным и Таниным. Кто занял последнее место?
(А) Таня
(Б) Аня
(В) Галя
(Г) Валя
(Д) Невозможно определить

Задача №9
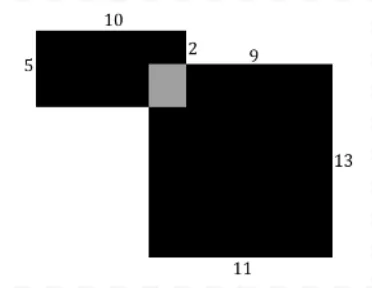
Чему равна сумма площадей черных фигур?

(А) 193
(Б) 181
(В) 187
(Г) 184
(Д) Невозможно определить

Задача №10
Когда астронавт Купер высадился на Далекую Ледяную планету, он был в три раза старше своей 11-летней дочери. Во сколько раз время на этой планете течет медленнее, чем на Земле, если Купер пробыл на планете 4 года (по местному времени), а, когда улетел, он уже был в три раза младше своей дочери?
(А) 9
(Б) 12
(В) 25
(Г) 45
(Д) Среди вышеперечисленных нет правильного ответа