IX олимпиада по математике прошла 24 октября 2021 года.
Задачи олимпиады
Задача №1
Назовем число красивым, если четных цифр в его записи в два раза меньше, чем нечетных. Существует ли два подряд идущих красивых числа?
Задача №2
Длины стороны треугольника равны трём простым числам. Его периметр равен 52 см. Чему равна каждая сторона треугольника?
Задача №3
Придумайте наибольшее натуральное число, все цифры которого различны, а все слова при записи этого числа по-русски, начинаются на одну и ту же букву.
Задача №4
В банке 12 мармеладных червячков красного цвета. Маша и Миша по очереди их достают из банки. Маша съела одного червячка, и положила взамен зеленого. Миша съел двух какихто червячков и положил в банку двух красных. Маша съела трех, положила трех зеленых. И так далее. Каждый раз съедалось на одного больше, причем Маша докладывала обратно только зеленых, а Миша только красных червячков. Все закончилось, когда Миша съел за раз все 12 червячков. Сколько червяков съели дети? Сколько среди них было съедено красных, а сколько зеленых?
Задача №5
Каких чисел можно составить из чётных цифр больше (цифры не должны повторяться), четырёхзначных или пятизначных и насколько?
Задача №6
На веревку длиной 24 метра упала согнутая проволока. При этом образовалось 4 квадрата. Найдите длину проволоки, если известно, что площадь каждого следующего квадрата в 4 раза больше, чем предыдущий. (На рисунке верёвка обозначена зелёным, проволока красным)
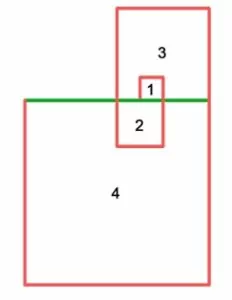
Задача №7
У Васи есть карточки с числами 3, 4, 6, 8, 12, 20, 28. Вася хочет разложить карточки в две кучки так, чтобы суммы чисел на карточках в кучках были равны (а количество карточек может различаться). Возможно, какие-то карточки придется выкинуть. Вася старается выкинуть как можно меньше карточек. Сколько он выкинул? Объясните, почему нельзя выкинуть меньше карточек. Покажите, как можно поделить карточки на две кучки.
Задача №8
Почему в отражении в зеркале право и лево меняется местами, а верх и низ не меняются?
Ответы на задачи №1-8 в формате разборов
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


