Задания Тринадцатой Олимпиады по математике Весна 2023 1 тур 4 класс

1 тур олимпиады по математике прошёл с 15 мая по 7 июня 2023 года

Задача №1
Коржик, Карамелька, Компот, Лапочка и Бантик стоят в ряд и держат 29 шариков. У котят слева от Карамельки 14 шариков, слева от Бантика 25, слева от Коржика — 19, слева от Лапочки — 3. Сколько шариков у Бантика?
(A) 5
(Б) 6
(В) 7
(Г) 4

Задача №2
Из дома к дереву с пчелами Винни-Пух бежал со скоростью 80 м/мин, а после того, как они его покусали во время полёта на шарике, еле-еле брёл домой уже со скоростью 16 м/мин. Какое расстояние от дома до дерева, если на весь путь туда-обратно (не считая общения с пчелами), у него ушел час?
(А) 400 метров
(Б) 800 метров
(В) 1200 метров
(Г) 1600 метров
(Д) 2000 метров

Задача №3
Частное площади квадрата и его периметра равно 4. Чему равна сторона квадрата?
(A) 1
(Б) 16
(В) 36
(Г) 12
(Д) 8

Задача №4
Пчелёнку на покрытие воском всех 6 граней единичного кубика (т. е. кубика, у которого все стороны равны 1) требуется 3 грамма воска. Сколько потребуется воска для покрытия со всех сторон данного тела?

(А) 50 грамм
(Б) 52 грамма
(В) 36 грамм
(Г) 44 грамма
(Д) 54 грамма

Задача №5
Найдите периметр фигуры, если все стороны фигуры пересекаются под прямым углом. (рисунок служит для иллюстрации, масштаб не соблюдён)

(A) 8
(Б) 10
(В) 12
(Г) 14
(Д) 16

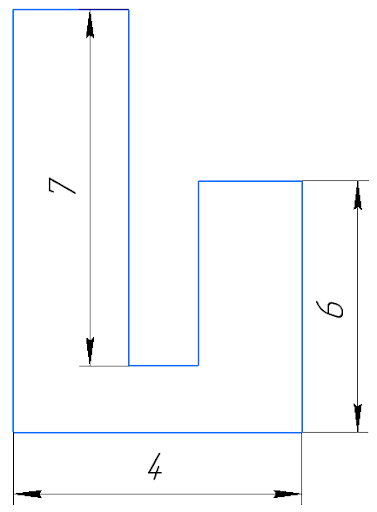
Задача №6
Три богатыря Илья, Алеша и Добрыня решили выяснить, кто из них самый быстрый. На полосе препятствий пока Илья делает 8 шагов, Алеша – 12 шагов. Пока Алеша делает 8 шагов, Добрыня — 12 шагов. Юлий посчитал, что Алеша и Добрыня вместе сделали 1080 шагов. Сколько шагов сделал Илья?
(A) 300
(Б) 320
(В) 160
(Г) 240

Задача №7
Числа от 1 до 10 расставлены в кругах так, что сумма в каждом круге одинаковая. Цифры 1,2,3,4,5,6,7 могут находиться в нескольких кругах одновременно. Какая цифра принадлежит всем четырем кругам одновременно?

(A) 4
(Б) 5
(В) 6
(Г) 7

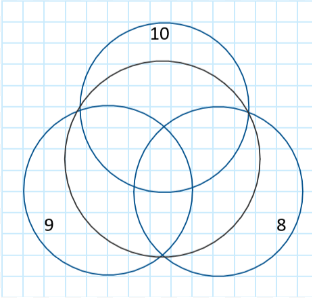
Задача №8
Сколько различных диагоналей можно провести в 100-угольнике?
(А) 10000
(Б) 50000
(В) 9700
(Г) 4850
(Д) 4900

Задача №9
В опросе приняли участия владельцы кошек и собак. Каждый из опрошенных владел ровно одним животным, которое могло быть длинношерстным или гладкошерстным. Количество владельцев длинношерстных кошек оказалось больше количества владельцев гладкошерстных собак, а число владельцев длинношерстных животных было меньше числа владельцев кошек.
Выберете самую многочисленную группу из перечисленных ниже:
(А) Хозяева собак
(Б) Хозяева короткошёрстных животных
(В) Хозяева кошек
(Г) Хозяева короткошёрстных кошек
(Д) Невозможно определить

Задача №10
Осьминоги всегда говорят правду, а одиннадцатиноги ­– всегда лгут. Однажды 12 многоного оказались в одной комнате, и рыбка Степан спросила у них, сколько осьминогов каждый из них видит вокруг (сам себя многоног не считает). Прозвучали ответы 1,4,3,1,4,3,4,3,1,4,4,5.
Сколько же на самом деле осьминогов в комнате?
(А) 3
(Б) 4
(В) 5
(Г) 6