Задания Тринадцатой Олимпиады по математике Весна 2023 2 тур 5 класс

Задача №1.

Автор: Тодоров Евгений

Тая и Женя очень любят сладкое. Готовясь к экзаменам, каждый из них купил по одинаковому набору шоколадок.
Известно, что они могут скушать целую шоколадку за 3 или 4 перекуса. Целого набора шоколадок Тае хватило на 41 перекус, а Жене — на 35 перекусов.
Сколько шоколадок в одном наборе?.

Задача №2.

Автор: Тодоров Евгений

За одной из пяти дверей спрятаны сокровища, а на самих дверях висят таблички: 1А, 1Б, 2А, 2В и 3Б.
Ника и Залина обладают безупречным логическим мышлением и хотят заполучить сокровища себе. Нике сказали только цифру, написанную на двери, за которой лежат сокровища, а Залине — только букву.
Им дали время подумать и спросили, какая дверь правильная. Обе промолчали.
Им дали ещё время и задали тот же вопрос вновь, и вновь обе промолчали.
Им снова дали поразмыслить и спросили в третий раз, и тогда обе девушки моментально дали правильный ответ и разделили сокровища поровну.
Известно, что если они знают ответ на вопрос, то сразу отвечают на него, а если нет — молчат.
За какой дверью были сокровища?

Задача №3.

Автор: Тодоров Евгений

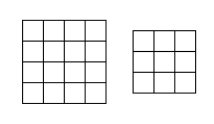
Дария наложила одну сетку 4х4 и одну сетку 3х3 с клеточками одинакового размера друг на друга и получила сетку, состоящую из 21 такой же клеточки. Затем она посчитала площадь каждого прямоугольника, который можно провести по линиям этой сетки.
Сколько различных значений получила Дария?

Задача №4.

Автор: Галиулина Варвара

У бельчонка новоселье. Ему нужно перетащить все свои орехи в новое дупло. В новом дупле есть три склада. За один раз бельчонок перетаскивает ровно два ореха из старого дупла в новое. Один орех он кладет на первый склад, другой на второй. Если на первом складе накопилось два или более орехов, то он перетаскивает все орехи из первого склада на второй. После этого, он пересчитывает орехи, лежащие на втором складе. Если их больше четырех, то все орехи со второго склада он перетаскивает на третий.
Сколько орехов в итоге оказалось на втором складе, если бельчонку пришлось сбегать до старого дупла и обратно 18 раз?

Задача №5

Автор: Санкеева Ольга

В волшебной стране живут маленькие человечки — жевуны. У мальчиков жевунов по 5 бубенчиков на одежде, у девочек по 7 бубенчиков, у взрослых — 8. На прогулку вышли 12 жевунов, у которых оказалось вместе 77 бубенчиков.
Сколько было мальчиков и девочек среди жевунов?
Найдите все варианты ответа.

Задача №6.

Автор: Тодоров Евгений

По трассе проходит забег на разные дистанции.
На самой трассе каждый километр стоит палатка, в которой участники забега могут взять воды. Разные участники могут делать забеги на разное количество километров, но начинаться и заканчиваться любой забег должен у какой-то палатки. Все участники всегда бегут с севера на юг. Палатку будем называть проходной для забега, если забег не начинается и не заканчивается у этой палатки, но проходит мимо неё. Оказалось, что та палатка, в которой дежурит волонтёр Настя, является проходной максимум для 36 различных маршрутов, а та, в которой дежурит Петя, является проходной максимум для 51 различного маршрута.
Забег какой максимальной длины можно сделать по этой трассе?

Задача №7.

Автор: Иванюк Дмитрий

У компании гномов 97 драгоценных камней на всех, причем у каждых двух гномов вместе не больше 9 драгоценных камней.
Какое наименьшее число гномов может быть в этой компании, если каждым камнем владеет ровно один гном?

Задача №8.

Автор: Тодоров Евгений

На доске написано число 30. Двое играют в игру. За один ход разрешается вычесть из числа на доске какой-то точный квадрат, не больший написанного числа, стереть старое число и написать вместо него полученную разность. Выигрывает тот, кто первым получит число 0.
Кто победит при правильной игре?