VII олимпиада по математике прошла 25 октября 2020 года.
Задачи олимпиады
Задача №1
В ряд выписали все числа от 1 до 99. Можно ли расставить между всеми числами знаки “+” или “–” так, чтобы полученное выражение равнялось нулю?
Задача №2
В кинотеатре, в целях соблюдения дистанции, в каждом ряду разрешили садиться на все места через одно. Остальные места демонтировали. Через неделю опять разрешили садиться на все места (из тех, что остались) через одно. А ещё через неделю опять разрешили садиться на все места (из тех, что остались) через одно. Оказалось, что в ряду стало в семь раз меньше мест, чем было изначально. Сколько мест в ряду было до соблюдения дистанции?
Задача №3
Перед вами икосаэдр. В его вершинах расставили числа от 1 до 12. На каждой грани записали сумму трёх чисел в ее вершинах. Могут ли числа на всех гранях быть равны?
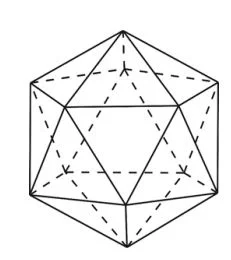
Задача №4
В одной сказочной стране в паспортном столе выходные дни: понедельник, среда, а также все числа месяца, которые не имеют других делителей кроме себя и единицы. Какое максимальное число дней подряд могут длиться выходные в паспортном столе?
Задача №5
Предположим, что в нашей галактике 100 миллиардов звёзд. Вокруг каждой звезды в среднем 10 планет. На каждой сотой планете есть жидкая вода. На каждой тысячной планете с жидкой водой зарождается жизнь. В одном из тысячи случаев жизнь становится разумной. Для простоты будем считать, что жизнь и разумная жизнь появляются в произвольный момент. Время существования нашей галактики 10 миллиардов лет. Среднее время существования разумной жизни на планете 1 миллион лет. Исходя из этих условий, сколько в среднем планет с разумной жизнью должно существовать в нашей галактике прямо сейчас?
Задача №6
Решите ребус. Каждая буква означает одну определенную цифру. Одинаковым буквам соответствуют одинаковые цифры. Разным буквам соответствуют разные цифры. Достаточно привести один пример.
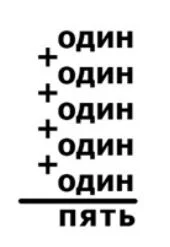
Задача №7
Разделите фигуру на три одинаковых по линиям сетки.
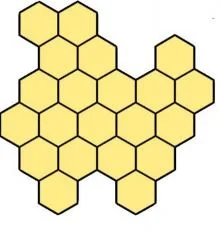
Задача №8
Собрались как-то 1000 человек. Сколькими способами можно выбрать из них 998 человек? (порядок не важен)
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


