Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 7 класс

На данной странице размещены олимпиадные задания с решением для 7 класса.
Олимпиада по математике прошла с 15 сентября по 2 октября 2022 года

Посмотреть ответы на все задания олимпиады

Посмотреть ответы на задания

Вопрос №	1	2	3	4	5	6	7	8	9	10	11	12	13
Ответ	В	Г	6000066779	12	Г	Г	В	1023469875	Д	А	2025	Д	Б

Задача №1
Числа от 1 до 9 разместите в квадратах так, чтобы были верными все неравенства. Что может стоять в центре?
Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 7 класс
(A) 3 или 4
(Б) только 4
(В) 4 или 5
(Г) только 5
(Д) 5 или 6

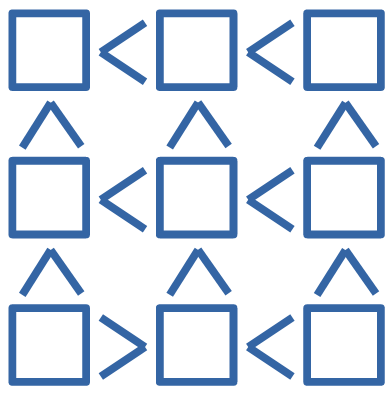
Задача №2
Решите ребус: БАО×БА×Б = 2002. Чему равна буква А?
(A) 1
(Б) 2
(В) 3
(Г) 4
(Д) Решений нет

Задача №3
Число составлено из цифр 0, 6, 7 и 9. Каждая используется разное число раз, большее нуля. Каким будет наименьшее число с таким свойством? (Введите число)

Задача №4
Решите уравнение в целых числах 3< |x| <10, где |x| — модуль числа (Введите количество решений)

Задача №5
Иван родился в Костромской губернии в 1878 году и прожил там 70 лет. Какой год для него не был бы високосным если бы он жил в Мюнхене, а не в Костромской губернии всю свою жизнь?
(A) 1880
(Б) 1892
(В) 1899
(Г) 1900
(Д) 1904

Задача №6
Фирма занимается изготовление прессованных топливных брикетов, которые делают из сухих опилок. Для выполнения заказа необходимо 4 тонны опилок с влажностью 10% (доля влаги в материале). Сколько килограмм опилок с влажностью 25% надо взять?
(A) 4500
(Б) 4600
(В) 4750
(Г) 4800
(Д) 4950

Задача №7
Петя построил замок из конструктора. В процессе работы он заметил, что все детали кратны какой-то величине. После построения он начертил свой замок на клетчатой бумаге так, чтобы самая маленькая фигурка занимала минимальное число клеточек. Вычислите — какая площадь замка в клеточках у него получилась.
Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 7 класс
(A) 224
(Б) 236
(В) 242
(Г) 248
(Д) 256

Задача №8
Найдите наименьшее натуральное число, делящееся на 375, в записи которого встречаются все 10 цифр.(введите это число)

Задача №9
Петя наблюдает за своим попугаем с утра и каждый день записывает результаты в тетрадку. Попугай делает одно из четырёх действий:
а) прыгает по клетке;
б) чистит пёрышки;
в) кушает;
г) говорит.
После 4х дней мама попросила посмотреть тетрадку. Сколько различных результатов наблюдений там могло быть?
(A) 16
(Б) 24
(В) 64
(Г) 120
(Д) 256

Задача №10
Отец и сын решили мерить расстояние между 2 деревьями. Чему оно равно если шагать они начали и закончили одновременно и в промежутке их следы совпали ещё 8 раз. Шаг отца 80 см, а сына 48.
(А) 21 м 60 см
(Б) 22 м 40 см
(В) 24 м 0 см
(Г) 24 м 80 см
(Д) 25 м 60 см.

Задача №11
Запишите год, ближайший к текущей дате, такой, что из цифр его составляющих переставляя их в разных порядках можно получить натуральные числа, делящиеся на числа от 1 до 10 включительно (не обязательно чтобы это было одно число, цифры можно использовать все или частично) Введите этот год

Задача №12
Фигура состоит из квадратов со стороной 1. Чему равен периметр этой фигуры?
Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 7 класс
(A) 14
(Б) 15
(В) 16
(Г) 17
(Д) 18

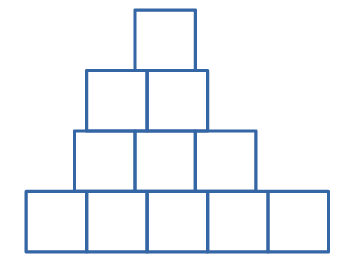
Задача №13
Когда четверых ребят спросили, сколько из них вчера дежурило в классе, Юля ответила, что никто, Валя — что только один человек, Кирилл — что два, а Никита— что три. Известно, что правду сказали только те, кто дежурил в классе. Сколько ребят вчера дежурили?
(A) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4