Задания Тринадцатой Олимпиады по математике Весна 2023 2 тур 7 класс

Задача №1.

Автор: Галиулина Варвара

Есть карточки с числами 123, 124, 134, 234 (с каждым числом — сколько угодно карточек).
Можно ли разложить их по кругу так, чтобы у каждой пары чисел, стоящих рядом, была одинаковая цифра, и каждая пара чисел с одинаковой цифрой встречалась рядом ровно один раз?

Задача №2.

Автор: Альперин

Про натуральные числа a, b, c известно, что: НОД(a;b)+НОД(b;c)+НОД(a;c)=(a+b+c)/2.
Докажите, что хотя бы одно из трёх чисел делится на другое.

Задача №3.

Автор: Галиулина Варвара

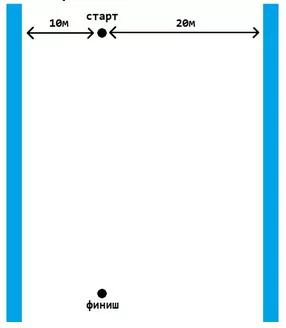
Два брата решили посоревноваться в беге «с нагрузкой» по следующим правилам: у каждого брата есть ведро, братья стартуют вместе и финишируют в указанной на рисунке точке. Но перед тем как бежать на финиш, братья должны добежать до каналов и зачерпнуть оттуда воду — младший до левого, а старший до правого. Каналы с водой параллельны, но от старта до левого канала 10 метров, а до правого — 20 метров. Прямая, на которой находятся старт и финиш, параллельна каналам.
Кто выиграет, если оба брата выбрали наилучшие (кратчайшие) пути, но старший бегает в 2 раза быстрее?

Задача №4.

Автор: Тодоров Евгений

В стране роботов в качестве валюты используются бины. Известно, что бывают монеты номиналом в 1, 4 и 8 бинов.
Сколькими различными способами можно набрать сумму в 80 бинов, пользуясь такими монетами?

Задача №5

Автор: Галиулина Варвара

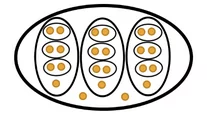
Гоблин Крюкохват хранит свои золотые монеты в большом мешке. Однажды, он захотел разложить их по более мелким мешочкам.
Он делает это так: если количество монеток в каком-нибудь мешке больше трёх, он высыпает их все и пересчитывает; если их количество делится на 3, поровну раскладывает их в три мешка поменьше; если же количество высыпанных монеток не делится на 3, то откладывает в сторону 1 или 2 монеты, чтобы оставшееся количество делилось на 3, поровну раскладывает оставшиеся в три мешка поменьше; потом все три мешка поменьше и отложенную 1 или 2 монеты (если они есть) складывает в исходный мешок обратно. Этот процесс он повторяет это до тех пор, пока может.
Сколько мешков понадобится, если у Крюкохвата 210 золотых монет?
Пример для 23-х монет показан на рисунке.

Задача №6.

Автор: Тодоров Евгений

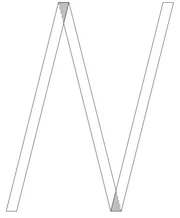
Полоску длины 2023 и ширины 23 сложили в форме буквы “N”, как показано на рисунке, причём углы, под которым складывали полоску в каждом из случаев, произвольны.
Какова минимальная суммарная площадь участков, закрашенных серым?

Задача №7.

Автор: Альперин

Трёхзначное натуральное число назовём крутым, если в нём можно переставить цифры так, что получится число, делящееся на 11. Если само число уже делится на 11, оно тоже является крутым.
Найдите количество крутых чисел.

Задача №8.

Автор: Тодоров Евгений

На доске написано число 30. Двое играют в игру. За один ход разрешается вычесть из числа на доске какой-то точный квадрат, не больший написанного числа, стереть старое число и написать вместо него полученную разность. Выигрывает тот, кто первым получит число 0.
Кто победит при правильной игре?