Задания Четырнадцатой Олимпиады по математике Осень 2023 2 тур 7 класс

Задача №1.
Автор: Тодоров Евгений

Яша и Зюзя изобрели свои температурные шкалы.
Яша принял за 0 температуру, при которой у него замерзает левая пятка, а 1 градус по его шкале — это то, насколько нагревается камешек, если Яша держит его в руке ровно минуту.
А Зюзя принял за 0 температуру, при которой он начинает шмыгать носом и чихать, а за 1 градус принимает то, как меняется температура железного шарика, если Зюзя дышит на него ровно минуту.
Каждый из изобретателей сделал термометр для своей шкалы и пошли мерить всё на свете. Оказалось, что если нагреть что-то на 1 градус по шкале Яши, то оно нагреется на 2 градуса по шкале Зюзи; а ещё оказалось, что 0 по шкале Зюзи равен 6 по шкале Яши.
Какая температура будет выражаться одинаковым числом градусов по обеим шкалам?

Задача №2.
Автор: Иванюк Дмитрий

Что больше 49! или (7!)⁸ ?
Пользоваться калькулятором для объяснения ответа недопустимо.

Задача №3.
Автор: Нилов

Даня написал на доске 4 различных натуральных числа. Федя для каждой пары чисел выписал отношение большего к меньшему (всего 6 чисел).
Сколько различных чисел могло получиться у Феди?
Для каждого варианта приведите пример 4 чисел и докажите, что других вариантов быть не может.

Задача №4.
Автор: Тодоров Евгений

Дан клетчатый квадрат 15×15. Разрежьте его на 16 прямоугольников так, чтобы из них можно было собрать любой прямоугольник с целыми сторонами от 1 до 15.

Задача №5
Автор: Тодоров Евгений

На волшебный турнир приехали 19 команд. Каждая команда в ходе турнира должна встретиться с каждой по одному разу. В какой-то момент капитан команды Годриковские львы заметил, что среди остальных команд все сыграли разное количество матчей, а опоздавшая на турнир команда Барсуки Хельги и вовсе ещё не успела ни с кем сыграть. Сколько матчей к этому моменту успела отыграть команда Годриковские львы?

Задача №6.
Автор: Тодоров Евгений

Произвольный треугольник разделён на 11 полосок одинаковой ширины, параллельных одной из сторон, как показано на рисунке. Известно, что суммарная площадь голубых полосок равна 330.
Чему равна площадь всего треугольника?

Задача №7.
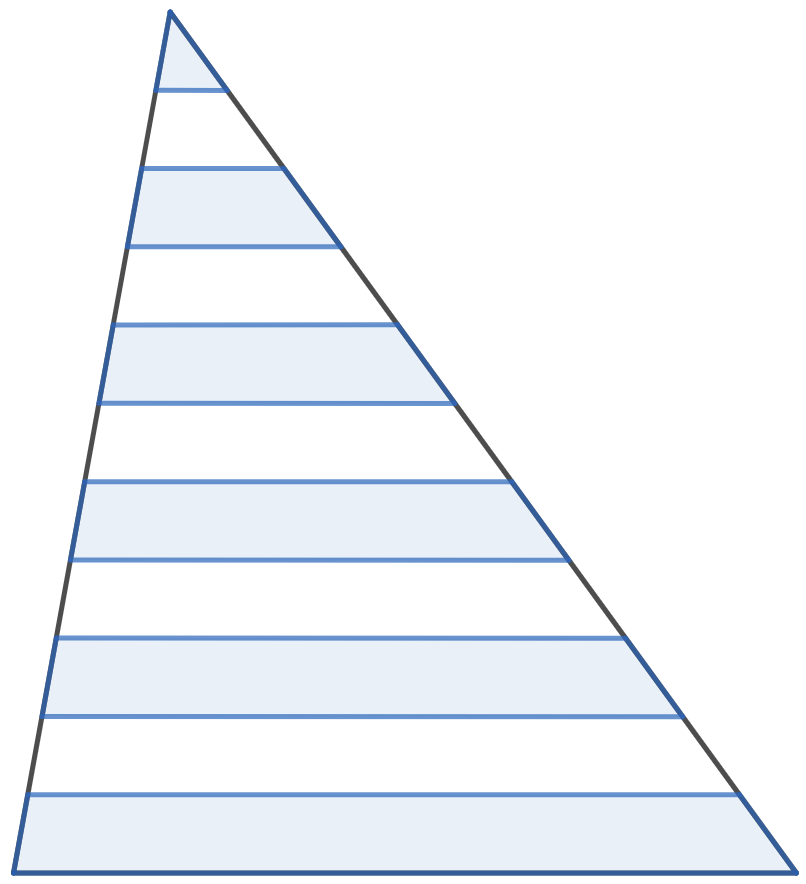
Автор: Тодоров Евгений

В четырёхугольнике ABCD углы B и D равны по 90°, а сторона BC имеет длину 52. Кроме того, перпендикуляр AH, опущенный на диагональ BD, делит её на отрезки BH и HD, равные 39 и 25 соответственно. Найдите длину стороны CD.

Задача №8.
Автор: Тодоров Евгений

У гномов есть особенный праздник, который называется пятисумье. Это день рождения гнома, в который ему исполняется количество лет, в пять раз большее, чем сумма цифр его года рождения. Например, у гнома, родившегося в 2000 году пятисумье наступит в 10 лет, а у родившегося в 1999 — в 140 (отметим, что гномы живут очень долго). Гномы-математики Регин и Радсвинн, родившиеся в XX и XXI веке соответственно, вычислили, что их пятисумье наступит в один день. Какой может быть разница в их возрастах?
Найдите все варианты ответа.