Задания II олимпиады по математике для 3-4 классов

Разделите фигуру вдоль линий сетки на три равные по форме и размеру части.

Антон, Боря, Вася, Гога и Даня встали в ряд. Подпишите имена мальчиков, если известно, что: Антон носит шорты в горошек. Боря стоит не с краю. Вася кудрявый. Гога в очках. Даня кудрявый. Вася стоит не с краю. Вася выше Бори. Боря стоит рядом с Антоном. задачи для второй олимпиады

На чёрно-белую вечеринку пришли ребята или в полностью черном костюме, или в полностью белом. Когда в финальном танце все встали в круг и взялись за руки, то выяснилось, что: тех, кто держат за руку мальчика и девочку — 6 человек; тех, кто держат за руку двух мальчиков — 5 человек; тех, кто держат за руку людей в костюмах разного цвета — 8 человек; тех, кто держат за руку только людей в чёрном — 4 человека. Кого на вечеринке больше девочек или тех, кто в белом? На сколько? Напишите ответ и объяснение.

Мистер Кот гуляет по роялю. Сначала он вступает на первую клавишу, потом на четвертую (первая плюс три), потом на девятую (четвертая плюс пять) и так дальше он прибавляет последовательные нечётные числа. Когда не хватает клавиш, кот спрыгивает вниз. На какую последнюю клавишу вступит Мистер Кот, если у рояля 57 клавиш? Напишите ответ и объяснение.

Петя и Аня решали головоломки. В конце занятия Оксана Евгеньевна спросила, сколько головоломок решили ребята.
Петя ответил: «Я решил половину количества головоломок, которые решила Аня, да ещё 10 штук».
Аня сказала: «Я решила столько же, сколько Петя, да ещё 20 штук».
Сколько всего головоломок решили Аня и Петя в сумме? Напишите ответ и объяснение.

Расставьте на шахматной доске 16 коней, чтобы каждый бил ровно 4 других.

Аня и Петя придумали по натуральному числу. Оказалось, что если их сложить, то получится 1345. Если Аня к концу своего числа припишет цифру 3, а Петя на конце своего числа вычеркнет цифру 2, то получившиеся числа будут одинаковые. Найдите задуманные числа. Напишите ответ и решение.

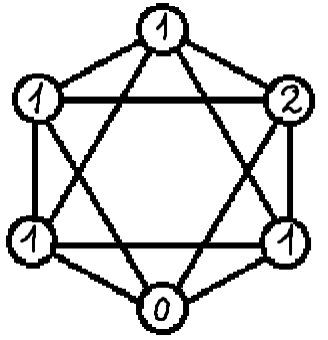
В кружочки расставлены числа как на картинке. За один ход можно взять три числа в вершинах какого-нибудь треугольника со сторонами, идущими по линиям, и прибавить к ним по 1. Можно ли такими операциями сделать все числа равными? Если можно, напишите как это сделать (алгоритм), если нельзя, объясните почему.