Задания 1-го тура XV олимпиады по математике для 6 класса

Чтобы впечатлить профессора Крошка Цахес сложил восемь подряд идущих чисел и записал результат на доску. Однако профессор сказал, что в вычислениях ошибка. Оказалось, что Крошка Цахес ошибся буквально на единицу. Какое число могло быть записано на доске?

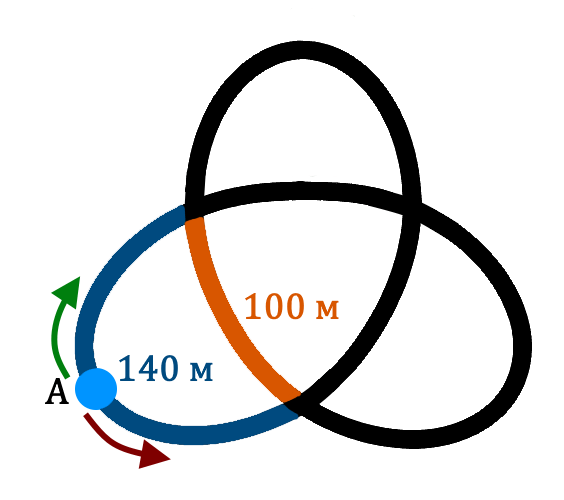
В городе N построили необычную беговую дорожку. Два спортсмена стартуют одновременно из точки А (середины синей дорожки), бегут в противоположных направлениях с одинаковыми скоростями. На развилках они могут поворачивать куда угодно, только не в обратном направлении. Каждый спортсмен пробежал по 2 километра. Чему равно наибольшее количество раз, которое они могли встретиться, не считая встречу на старте, если за всю тренировку они ни разу не бежали рядом?

Маленькая обезьянка съедает все фрукты с дерева за 6 часов, а ее мама и папа (каждый по отдельности) съедают в два раза быстрее. За сколько времени семья обезьянок вместе съест все фрукты с дерева?

На сколько квадратов (не обязательно одинаковых) нельзя разрезать квадрат?

Во 2-м «А» классе 30 учеников, среди них – Вася, Коля, Петя и Толя. Каждый из четырех мальчиков дружит ровно с пятью своими одноклассниками. При этом, у Васи и Коли 4 общих друга, у Коли и Пети 1 общий друг, у Пети и Толи 2 общих друга, у Васи и Толи 1 общий друг. Какое наименьшее количество детей, которые не дружат ни с Васей, ни с Колей, ни с Петей, ни с Толей, могут быть в классе (сам с собой человек дружить не может)?

Несколько игроков участвовали в турнире GeoGuesser. Каждый сыграл с каждым по одному разу. За одну игру каждый из двух игроков может получить любое количество баллов от 0 до 10. Известно, что в играх было задействовано 5 карт, и на каждой карте прошло одинаковое количество раундов. Какое минимальное количество игроков должно было быть, чтобы гарантировано нашлась карта, на которой дважды набрали одинаковое количество баллов?

Когда цирк уехал клоунам Александру, Дмитрию и Максиму пришлось искать новую работу. Каждый из друзей решил попробовать освоить две разных специальности: переводчик, математик, программист, дизайнер, оперный певец, инженер. Известно, что:
• Программист выгуливал собаку дизайнера.
• Математик и инженер вместе с Александром любят ходить на рок-концерты.
• Программисту не понравился психолог, к которому ходит математик.
• Дмитрий принес тортик на день рождения инженера.
• Дизайнер продал переводчику заглохшую машину.
• Максим готовит пельмешки быстрее, чем Дмитрий и дизайнер.
Какие новые специальности решил освоить Максим?

В жаркий день Ллойд и Гарри решили раскопать себе ямы, чтобы спрятаться от солнца. Через час они прервались и выяснили, что Ллойд успел выкопать 9 кубометров, а Гарри – всего 6. После перерыва они снова принялись за дело, но Гарри обиделся и стал скидывать выкопанную землю в яму Ллойда, а Ллойд, в отместку - в яму Гарри. Какого размера будет яма Ллойда, к моменту, когда яму Гарри полностью засыплет?

Ниф-Ниф, Нуф-Нуф и Наф-Наф задумали три числа, цифры которых различны: трёхзначное, четырёхзначное и пятизначное. Оказалось, что у числа Ниф-Нифа все цифры нечётные и оно в 15 раз больше числа Нуф-Нуфа. Какое число задумал Наф-Наф, если известно, что оно равно сумме чисел Ниф-Нифа и Нуф-Нуфа?

Катя возвела двойку в тридцатую степень. Екатерина Возвела пятёрку в двадцатую степень. Катюша перемножила эти два числа. А Кейт вычислила сумму цифр полученного большого числа и умножила на количество нулей в нём же. Какой результат получился у Кейт?