Дарим курс
Математика: перезагрузка

Скидка действует только до 23:59 сегодня. Успейте воспользоваться!
X олимпиада по математике прошла 30 января 2022 года.
Задача №1
Санта и Эльфы готовят подарки детям. Причем всегда подарки дарят всем детям в равном количестве. Все подарки, которые раздать не получилось, забирает Гринч. Пересчитав число подарков в мешке Санта заметил, что если их раздавать пятерым, то Гринч получит два подарка. А если четверым, то один подарок. А если троим, то и вовсе Гринчу ничего не останется. Какое наименьшее число подарков могло быть в мешке?
Задача №2
Из ряда натуральных чисел изъяли все числа, которые являются степенями натуральных чисел. (Являются степенями с показателем больше 1) Какое число стоит на 123 месте среди оставшихся?
Задача №3
На нескольких карточках Вася написал цифру, а с оборота букву (если цифры равны, то буквы одинаковы, если цифры различны – буквы разные). Вася считает сумму цифр на карточках. Если выложить слово ЛОМ получится сумма 5, МОЛВА – 21, ВОЛ – 13, ВИНА – 28. А что получится в сумме, если выложить слово ЛИАНА?
Задача №4
В прямоугольном параллелепипеде длина равна 4 м, ширина — 8 м. Также известно, что периметры двух каких-то смежных граней параллелепипеда отличаются на 2 м. Найти объем параллелепипеда.
Задача №5
Десять точек расположены так, как показано на рисунке. Какое наименьшее число точек нужно стереть, чтобы не нашлось правильного треугольника с вершинами в этих точках?
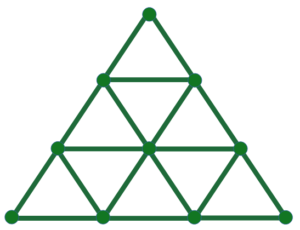
Задача №6
Известно, что A, B, C натуральные числа, все они принадлежат множеству простых или составных чисел. Найдите все решения уравнения AxBxC=2022
Задача №7
Бак был полон воды. Эту воду поровну перелили в четыре бидона. Оказалось, что в первом бидоне вода заняла треть его объёма, во втором бидоне вода заняла 40% его объёма, в третьем бидоне – 3/7 его объёма, а в четвёртом 7/9. Бак и все четыре бидона вмещают по целому числу литров. При каком наименьшем объёме бака возможна такая ситуация?
Задача №8
Докажите, что ![]() — составное число.
— составное число.
Задача №9
Квадрат с периметром 20 см разделили на 4 одинаковых треугольника и один черный квадрат. Площадь треугольника равна 6см2 Найти стороны треугольника. Если они целочисленные. Без предположений и перебора.

Задача №10
Из Цзюцюань в Ханчжоу, расположенные друг от друга на расстоянии 3000км, требуется перевезти 300 тонн груза. Товарный поезд едет со скоростью 100км/ч и имеет грузоподъемность 60 тонн. Скорый поезд едет со скоростью 120км/ч и имеет грузоподъемность 50 тонн. Какой из поездов быстрее перевезет весь груз в Ханчжоу?
Решения и ответы

Пробная олимпиада
Пройдите пробную олимпиаду по математике для 1–9 классов.
1-й тур: 15 – 29 сентября
2-й тур: 20 июля
Олимпиада по математике
Девятнадцатая международная олимпиада по математике
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Зарегистрироваться
Бесплатно


