Задания 2-го тура XV олимпиады по математике для 6 класса
2 тур XV олимпиады по математике прошел 25 февраля 2024 года.
Задачи олимпиады
Задача №1
Сколькими способами можно представить 2024 в виде (a-b)*(a+b), где a и b - натуральные числа?
Иванюк Д. В.
Задача №2
Три брата купили две одинаковые по цене коллекционные машинки совместно. На одну они потратили деньги в отношении 7:8:6, а на другую — в отношении 5:6:4. При этом, один из братьев отдал за первую машинку на 120 рублей больше, чем за вторую. Сколько стоила одна машинка?
Ерина Ю. Ю.
Задача №3
На сторонах BC и СD прямоугольника ABCD отмечены точки M и K. Известно, что стороны прямоугольника равны 17 и 27. Известно также, что периметр треугольника ABM равен 47, периметр MCK равен 37, а периметр MDA равен 57. Чему равен периметр треугольника AMK?
Задача №4
Франциска бежит со скоростью 7 км/ч. В 15:00 она получает на свои умные часы сообщение с напоминанием о том, что в 15:30 у нее назначена встреча с подругой. Она бежит домой тем же путем с удвоенной скоростью, а затем ей требуется еще 10 минут, чтобы принять душ и переодеться. Затем она едет со скоростью 3 км/ч к своей подруге, которая живет в 250 м. от нее, и приходит вовремя.
Иванюк Д. В.
Задача №5
У Васи есть два набора карточек с числами от 1 до 100. Он разложил первый набор в ряд (в случайном порядке), потом нарисовал под каждым числом дробную черту и под каждой чертой положил по одному числу из второго набора. Получившиеся 100 дробей он сложил. Докажите, что он получил результат не менее 100.
Галиулина В. Н.
Задача №6
Андрей заказал пиццу, которая согласно заявленным характеристикам, должна была быть 50 сантиметров в диаметре. Однако, произведя измерение готового продукта, Андрей заметил, что фактический размер пиццы составил 47 см в диаметре. Андрей был недоволен, и потребовал вернуть ему сумму денег, эквивалентную недостающей части пиццы. Какую сумму денег должны вернуть Андрею, если ее стоимость 1000 рублей? Ответ округлите до целого числа рублей.
Миронов Д. Р.
Задача №7
У Аркаши-фокусника есть 600 белых шариков и 1200 чёрных. Он разложил их по пяти мешкам (в каждом лежат только белые или только чёрные шарики). Теперь он хочет достать один белый шарик с первой попытки. Как ему это сделать? Вес мешков указан на картинке. Все шарики весят одинаково.
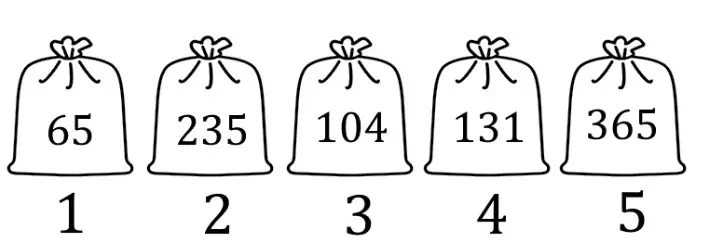
Галиулина В. Н.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



