Задания 1-го тура XVI олимпиады по математике для 6 класса
1 тур XVI олимпиады по математике прошел с 25 сентября по 13 октября 2024 года.
Задачи олимпиады
Задача №1
Сосчитайте сколько четырёхугольников в этой фигуре?
(А) 16 (Б) 22 (В) 28 (Г) 37 (Д) 41
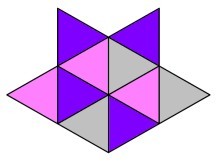
Иванюк Е. В.
Задача №2
Найдите остаток от деления суммы 1! + 2! + 3! + ... + 14! на 14.
(А) 3 (Б) 5 (В) 7 (Г) 8 (Д) 10
Тодоров Е. И.
Задача №3
Если сурикат встанет под пальму, то от его макушки до макушки пальмы будет 180 сантиметров. А если сурикат встанет на пальму, то от его макушки до земли будет 240 сантиметров. Какого роста сурикат?
(А) 25 (Б) 28 (В) 30 (Г) 33 (Д) 36
Тодоров Е. И.
Задача №4
На доске написано число 125292521. У написанного числа выбираются две соседние цифры, если ни одна из них не равна нулю, из каждой вычитается по единице и выбранные цифры меняются местами (например, 125292521 можно превратить в 141292521). Какое наименьшее число может быть получено в результате таких операций?
(А) 100000000 (Б) 101010101 (В) 105050301 (Г) 101070301 (Д) 104170210
Тодоров Е. И.
Задача №5
Лизе очень нравится номер текущего года, а ещё ей нравится применять к числам одинаковые алгоритмы. Поэтому однажды она написала на листке число 24, потом умножила его на 7, вычла 3 и у результата стёрла все цифры, кроме последней. С полученным числом она проделала те же действия. А потом ещё и ещё раз. Всего Лиза проделала 2024 таких операции. Какое число получилось у неё в результате?
(А) 1 (Б) 2 (В) 4 (Г) 5 (Д) 24
Тодоров Е. И.
Задача №6
В четыре бокала налит виноградный сок. Первый и второй бокал заполнен на 3/4, третий — на 5/6, четвёртый — на 1/3. Золушка решила сделать так, чтобы всем гостям сока досталось поровну. За один раз она может перелить сок из одного бокала в другой так, чтобы второй бокал оказался заполнен до краев, либо так, чтобы сока в бокалах стало поровну. За какое минимальное количество шагов она может это сделать?
(А) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
Галиулина В. Н.
Задача №7
На бал пришли 4 дамы и 4 кавалера. Камердинер хочет запускать гостей внутрь таким образом, чтобы любая дама могла найти кавалера для танца, как только она зайдёт в зал. Для этого камердинер просит дам и кавалеров выстроиться в очередь. Сколькими способами он может составить такую очередь? (варианты, в которых местами меняются только несколько кавалеров или только несколько дам, считать одинаковыми)
(А) 4 (Б) 12 (В) 14 (Г) 24 (Д) 70
Тодоров Е. И.
Задача №8
Какова сумма цифр наименьшего шестизначного числа, делящегося на 99?
(А) 9 (Б) 18 (В) 27 (Г) 36 (Д) 45
Миронов Д. Р.
Задача №9
За плохую работу Жене понизили зарплату на p процентов, но в следующем месяце он постарался, и зарплату повысили на те же самые p процентов. Однако оказалось, что теперь его зарплата всё равно на 4 процента ниже, чем была до понижения. Чему равно p?
(А) 2 (Б) 4 (В) 10 (Г) 20 (Д) 48
Тодоров Е. И.
Задача №10
Числа зашифрованы словами КУЛАК, КУЛИК, ЛАК и ЛИК. Одинаковыми буквами обозначены одинаковые цифры, разными — разные. Известно, что ровно одно из этих чисел больше 10290, и ровно одно из них меньше 240. Найдите, чему равно А + И.
(А) 1 (Б) 3 (В) 10 (Г) 12 (Д) 13
Галиулина В. Н.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Г | Б | В | Б | В | В | В | Б | Г | Г |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


