Задания 1-го тура XVI олимпиады по математике для 8 класса

Когда пассажирский поезд идёт навстречу товарному, он проезжает мимо него в 3 раза быстрее, чем когда поезда идут в одном направлении. За сколько минут товарный поезд проедет мимо стоящего пассажирского, если пассажирский поезд проезжает мимо стоящего товарного за 2 минуты?

Во дворце Чудовища каждая дверь ведёт из одной комнаты в другую. Красавица заметила, что, если любым способом закрыть не более чем 1/3 всех дверей, то из любой комнаты всё ещё можно будет попасть в любую другую. Какое наибольшее количество комнат может быть во дворце?

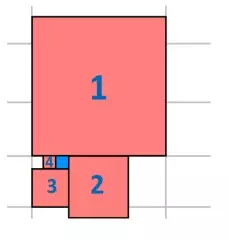
На рисунке изображено 5 квадратиков. Известно, что сторона самого большого равна 11, второй квадрат находится посредине стороны первого, третий — посредине стороны второго, четвёртый — посередине стороны третьего. Чему равна площадь голубого квадратика?

Каким будет минимальный простой делитель данного выражения:2024²⁰²⁴ - 2023²⁰²³ + 2022²⁰²² - … + 4⁴ - 3³ + 2² - 1¹

На станции за южным полярным кругом было 8 исследователей, но одного из них подменил пришелец из космоса. Каждый человек знает, кто пришелец, но слишком напуган чтобы говорить правду. Инспектор, который прибыл на станцию чтобы выявить опасного инопланетянина, может выделить любую группу людей (не меньше двух) и тайно опросить всю группу, то есть спросить у каждого из них, есть ли среди них пришелец. Люди на этот вопрос ответят правду, а пришелец может ответить правду, а может солгать. За какое наименьшее количество опросов инспектор может гарантированно определить пришельца?

Вычислите. Скобками, как водится, обозначается период дроби, то есть цифры, которые после запятой повторяются бесконечно много раз

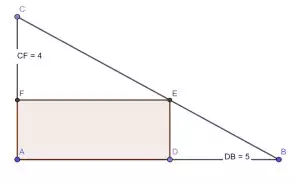
Внутри прямоугольного треугольника ABC нарисован прямоугольник ADEF, причём известно, что CF = 4, а DB = 5. Чему равна площадь прямоугольника ADEF?

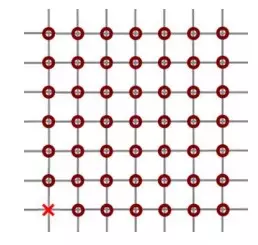
Рон Уизли (обозначен красным крестиком) может кинуть квоффл в любое кольцо (если на линии нет других колец). После попадания в кольцо мяч тут же отлетает влево или вправо под углом 90°. В какое максимальное количество колец Рон может забить голы за один бросок (если ему сильно повезёт)?

Длины сторон прямоугольника являются целыми числами. После того, как одну из сторон увеличили на 2, а вторую увеличили на 4, площадь прямоугольника увеличилась ровно в 3 раза. Какое максимальное значение может принимать площадь исходного прямоугольника?

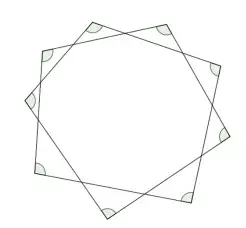
Ведьмочка Соня нарисовала на земле магическую девятиугольную звезду. Известно, что колдовство получится только в том случае, если она правильно назовёт сумму зелёных углов. Помогите Соне совершить колдовство и найдите нужную сумму.