Задания 1-го тура XVI олимпиады по математике для 9 класса
1 тур XVI олимпиады по математике прошел с 25 сентября по 13 октябя 2024 года
Задачи олимпиады
Задача №1
Во дворце Чудовища каждая дверь ведёт из одной комнаты в другую. Красавица заметила, что, если любым способом закрыть не более чем 1/3 всех дверей, то из любой комнаты всё ещё можно будет попасть в любую другую. Какое наибольшее количество комнат может быть во дворце?
(А) 4 (Б) 5 (В) 12 (Г) 48 (Д) Сколь угодно много
Галиулина В. Н.
Задача №2
Каким будет минимальный простой делитель данного выражения: 20242024 - 20232023 + 20222022 - … + 44 - 33 + 22 - 11
(А) 1 (Б) 2 (В) 3 (Г) 5 (Д) 2021
Миронов Д. Р.
Задача №3
На рисунке изображено 5 квадратиков. Известно, что сторона самого большого равна 11, второй квадрат находится посредине стороны первого, третий — посредине стороны второго, четвёртый — посередине стороны третьего. Чему равна площадь голубого квадратика?
(А) 1 (Б) 9/16 (В) 9/4 (Г) 81/100 (Д) 121/144
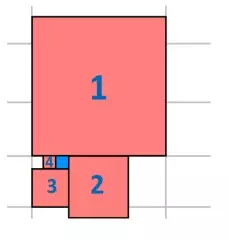
Галиулина В. Н.
Задача №4
Сколько корней имеет уравнение:
(А) ни одного (Б) один (В) два (Г) три (Д) больше трёх
Миронов Д. Р.
Задача №5
Ведьмочка Соня нарисовала на земле магическую девятиугольную звезду. Известно, что колдовство получится только в том случае, если она правильно назовёт сумму зелёных углов. Помогите Соне совершить колдовство и найдите нужную сумму.
(А) 360° (Б) 540° (В) 720° (Г) 900° (Д) 1080°
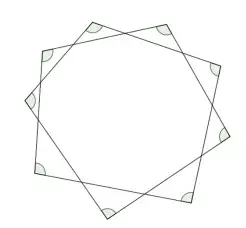
Тодоров Е. И.
Задача №6
Найдите наибольшее значение выражения:
(А) 50 (Б) 75 (В) 100 (Г) 125 (Д) 200
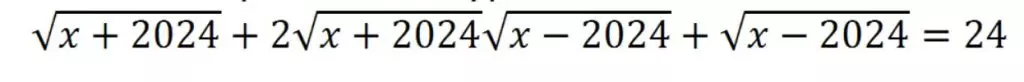
Задача №7
За плохую работу Жене понизили зарплату на p процентов, но в следующем месяце он постарался, и зарплату повысили на те же самые p процентов. Однако оказалось, что теперь его зарплата всё равно на 4 процента ниже, чем была до понижения. Чему равно p?
(А) 2 (Б) 4 (В) 10 (Г) 20 (Д) 48
Тодоров Е. И.
Задача №8
Прямоугольника с какими периметром и площадью не существует?
(А) P = 25, S = 38,5 (Б) P = 22, S = 28 (В) P = 19, S = 21 (Г) P = 12, S = 13 (Д) P = 28, S = 4
Тодоров Е. И.
Задача №9
Рон Уизли (обозначен красным крестиком) может кинуть квоффл в любое кольцо (если на линии нет других колец). После попадания в кольцо мяч тут же отлетает влево или вправо под углом 90°. В какое максимальное количество колец Рон может забить голы за один бросок (если ему сильно повезёт)?
(А) 5 (Б) 13 (В) 22 (Г) 25 (Д) 28
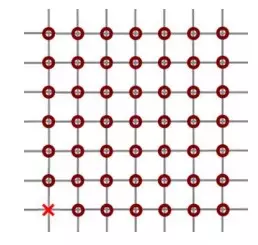
Галиулина В. Н.
Задача №10
Шесть машин едут из деревни Вилларибо в деревню Виллабаджо. Через час они выстроились на шоссе в обратном порядке. Известно, что машина, которая идет первой совершила ровно на 7 обгонов меньше, чем все остальные машины вместе взятые. Сколько обгонов совершила машина, которая сейчас едет четвертой, если она и машина, которая идет впереди нее, совершили одинаковое количество обгонов?
(А) 3 (Б) 4 (В) 5 (Г) 8 (Д) 10
Галиулина В. Н.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Б | Б | А | А | Г | В | Г | Г | В | А |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



