Задания 2-го тура XV олимпиады по математике для 9 класса
2 тур XV олимпиады по математике прошел 25 февраля 2024 года
Задачи олимпиады
Задача №1
Сколькими способами можно представить 2024 в виде (a-b)*(a+b) где a и b - целые числа?
Иванюк Д. В.
Задача №2
Андрей заказал пиццу, которая согласно заявленным характеристикам, должна была быть 50 сантиметров в диаметре. Однако, произведя измерение готового продукта, Андрей заметил, что фактический размер пиццы составил 47 см в диаметре. Андрей был недоволен, и потребовал вернуть ему сумму, эквивалентную недостающей части пиццы. Какую сумму должны вернуть Андрею, если ее стоимость 1000 рублей? Ответ округлите до целого числа рублей.
Миронов Д. Р.
Задача №3
Двоечник Вася уже в начале ноября имел три двойки, четыре тройки, одну четверку, и одну пятерку (за то, что выучил наизусть весь параграф по теме "среднее арифметическое натуральных чисел"). Воодушевившись текущим успехом, Вася решает получить пятерку по математике за всю вторую четверть, даже не смотря на свои предыдущие отметки. Сможет ли Вася добиться своей цели, если до конца четверти еще целых тридцать уроков по математике? (на одном уроке нельзя получить больше одной оценки, а пятерка за четверть выставляется только при среднем балле от 4.5).
Миронов Д. Р.
Задача №4
Ваня купил акции двух российских компаний и всего потратил на них 10 тыс.руб. Через год стоимость акций первой компании возросли на 20%, а второй упали на 10%. Ваня продал все акции и после налогового вычета в 2% его прибыль составила 584 рубля. Сколько бы Ваня заработал, если бы акции второй компании не упали в цене?
Ерина Ю. Ю.
Задача №5
В трапеции высота равна 15, а диагонали — 17 и 39. Чему равна площадь этой трапеции?
Задача №6
Игральный кубик бросили четыре раза. Какова вероятность того, что сумма чисел после четырех подбрасываний будет равна 24 (ответ округлите до тысячных)
Задача №7
У Алисы есть бумага для оригами двух её любимых цветов: тёмно-синего и чёрного. Она хочет сложить пять различных фигурок так, чтобы среди них была хотя бы одна тёмно-синяя и хотя бы одна чёрная фигурка. Сколькими способами она может это сделать?
Тодоров Е. И.
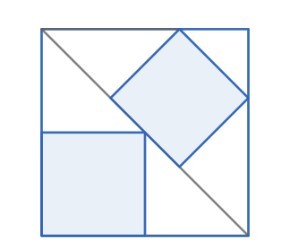
Задача №8
В большой (белый) квадрат вписали два синих так, как показано на рисунке. Найдите отношение площади большего синего квадрата к меньшему.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


