Задания 2-го тура XVI олимпиады по математике для 3 класса
2 тур XVI олимпиады по математике прошел 27 октября 2024 г
Задачи олимпиады
Задача №1
В стране Дружбы все дороги платные. Но платят тому, кто по ним едет, и в качестве платы выступают конфеты. Элли выехала из города А. И когда она приехала в город Г, у нее осталось 7 конфет. Сколько конфет у нее было в начале пути, если на каждой дороге она съедала по 3 конфеты, и ни по какой дороге она не проезжала дважды? (Рядом с каждой дорогой указано, сколько конфет платят тому, кто по ней проезжает)
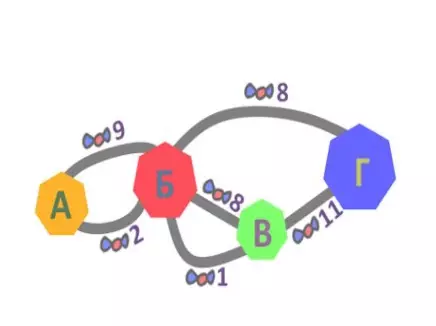
Галиулина В. Н.
Задача №2
В 2024 году сумма трех первых цифр равна четвертой (2 + 0 + 2 = 4). А сколько таких лет ещё от 2025 до 2099 года
Галиулина В. Н.
Задача №3
Банка с вареньем весила 6 кг. Когда Карлсон съел половину варенья, его вес стал равен 89 кг, а вес банки с вареньем – 4 кг. Сколько будет весить Карлсон, когда доест варенье до конца?

Галиулина В. Н.
Задача №4
Мэйбл купила коробку шоколадных конфет в подарок своему брату Дипперу (конфеты в ней лежали в два ряда, в каждом – одинаковое количество). Однако, по дороге не удержалась и съела несколько штук из второго ряда. Первый ряд Мэйбл не тронула. Если Диппер съест пять конфет, начиная с первого ряда, то во втором будет три конфеты. Если же он съест столько же, начиная со второго ряда, то в первом ряду будет пять конфет. Сколько конфет получил в подарок Диппер?
Галиулина В. Н.
Задача №5
Две команды участвуют в эстафете (в каждой команде поровну участников). После того, как каждую четвертую девочку из первой команды перевели во вторую, а каждую пятую девочку из второй команды перевели в первую, девочек в первой и второй команде стало поровну (а участников в обеих командах по-прежнему, одинаковое количество). Где изначально было больше мальчиков?

Галиулина В. Н.
Задача №6
Слова КОТ, ТОК и ЁЖ можно записать в строку, задействовав минимум семь букв (см. картинку). А какое наименьшее количество букв потребуется, чтобы также записать слова ПОКРОВ, РИС, КАРП, СЛЕПОК и КЕДР? Ответ объясните.

Галиулина В. Н.
Задача №7
Все сосуды имеют одинаковую форму, но разную высоту. Посередине каждого сосуда есть трубочка, соединённая с верхом следующего по величине сосуда. Второй сосуд слева полностью вмещает 48 миллилитров (до краёв)? Сколько нужно залить воды в самый большой сосуд, чтобы самый маленький наполнился до краёв?

Галиулина В. Н.
Задача №8
На заборе написано пять высказываний: Ровно одно из соседних утверждений истинно. Ровно одно из соседних утверждений истинно. Ровно одно из соседних утверждений истинно. Ровно одно из соседних утверждений истинно. Ровно одно из соседних утверждений истинно. Сколько среди высказываний истинных, если известно, что среди них есть как истинные, так и ложные? Ответ объясните.
Галиулина В. Н.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



