Задания 2-го тура XVI олимпиады по математике для 8 класса
2 тур XVI олимпиады по математике прошел 27 октября 2024 года
Задачи олимпиады
Задача №1
У Петра было некоторое количество рублей и копеек, причём изначально копеек было не больше 100. После того, как Пётр потратил 75% всех своих денег, у него осталось вчетверо меньше рублей, чем было копеек, и вдвое больше копеек, чем было рублей. Какую сумму потратил Пётр?
Тодоров Е. И.
Задача №2
Шестизначное число заканчивается на цифру 7, а если эту цифру переставить с последнего места на первое, число увеличится в 4 раза. Чему было равно изначальное число?
Тодоров Е. И.
Задача №3
В треугольнике АВС угол А равен 90°, точка М лежит на АС так что ВМ=МС=4. Угол ВМС равен 120°. Найдите площадь треугольника АВС.
Ерина Ю. Ю.
Задача №4
На рисунке изображён квадрат ABCD. Точки E, F, G, H являются серединами сторон квадрата. Внутри трёх четырёхугольников указана их площадь. Найдите диагональ исходного квадрата. В ответе укажите квадрат этого числа.
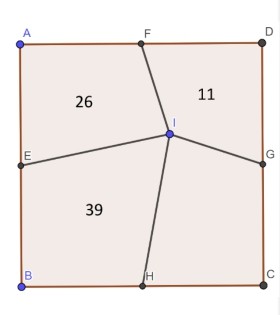
Миронов Д. Р.
Задача №5
Круг разбит на 8 одинаковых секторов. Будем называть маленьким кусочек, равный одному сектору круга (с углом 45°), а большим - кусочек, равный двум склеенным секторам круга (с углом 90°). Замощением называется способ положить большие и маленькие кусочки на круг так, чтобы края кусочков совпадали с линиями разреза на круге, а сами кусочки покрывали круг целиком и в один слой. Если два замощения можно совместить поворотом, мы всё равно будем считать их различными. Сколько различных замощений круга существует?
Тодоров Е. И.
Задача №6
Хоккеист Никита запустил шайбу из левого нижнего угла прямоугольного поля, длина нижнего борта которого равна 20 метров, а длина левого - 21 метр. Шайба прилетела в правый борт, отскочила от него, ударилась о верхний борт, потом ударилась о левый борт, и, наконец, прилетела точно в правый нижний угол. Известно, что шайба отлетает от бортов под тем же углом, под которым прилетает в них. Чему равно расстояние от левого верхнего угла поля до места на левом борте, от которого отскакивала шайба?

Тодоров Е. И.
Задача №7
Байкеры Андрей, Борис и Эрик выехали из пункта А в пункт Б в одно и то же время и с одинаковой скоростью. На половине пути Эрик засмотрелся на лисичку, пропустил поворот, случайно свернул в лес, где на 2 часа потерялся в тропинках, а потом вернулся на нужную дорогу на расстоянии 2/3 всего пути от пункта Б, удвоил скорость и прибыл на место на 20 минут позже Андрея. Байк Бориса сломался после 1/4 пройденного расстояния, Борис уселся чинить его, а когда починил - вскочил в седло и с утроенной скоростью поехал к пункту Б и прибыл на место на 20 минут раньше Андрея. Андрей проехал всю дорогу с постоянной скоростью и без приключений. Сколько времени Борис потратил на починку байка?

Тодоров Е. И.
Задача №8
В прошлом году математику Джону раз в месяц снилось некоторое натуральное число, причём каждый раз новое. В новогоднюю ночь Джон записал все двенадцать приснившихся ему чисел на листе бумаги. Верно ли, что среди них всегда можно выбрать четыре различных числа a, b, c и d так, чтобы произведение (a-b)*(c-d) делилось на 99?
Тодоров Е. И.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


