Задания 1-го тура XVII олимпиады по математике для 3 класса
1 тур XVII олимпиады по математике прошел с 21 января по 9 февраля 2025 г.
Задачи олимпиады
Задача №1
Клетки доски 3х3 закрашены в шахматном порядке (5 белых, 4 черных). В клетках доски записаны числа от 1 до 9 по одному разу. Оказалось, что суммы цифр в квадратах 2х2 равны 16, 22, 23, 27, а в центральной клетке таблицы расположена цифра 7. Чему равна сумма цифр в черных клетках?
А) 21 Б) 22 В) 32 Г) 60

Задача №2
Однажды крокодил Гена купил несколько булочек. Со ста рублей у него осталось 48 рублей сдачи. Булочки ему так понравились, что в следующий раз он купил максимальное возможное количество булочек на 100 рублёвую купюру. У него осталось 22 рубля сдачи. Найдите стоимость булочки, если она стоит целое количество рублей?
А) 52 Б) 39 В) 13 Г) 26
Галиулина В. Н.
Задача №3
Щенок Мяу тяжелее котёнка Гав на два килограмма, но легче бегемотика Моти на четыре килограмма. Все вместе они весят семнадцать килограмм. Сколько весят бегемотик Мотя и котёнок Гав вместе?
А) 10 Б) 11 В) 12 Г) 13
Гавва А. С.
Задача №4
В журнале «Супер киборги» есть три выпуска. К первому выпуску прилагаются голова, туловище и руки робота, ко второму — туловище, ноги и голова, а к третьему — руки и ноги. Какое наименьшее количество журналов нужно купить Денису, если он хочет собрать армию из пяти таких роботов?
А) 6 Б) 7 В) 8 Г) 10
Галиулина В. Н.
Задача №5
Для класса было закуплено 228 ручек и 190 карандашей. Пишущие принадлежности были розданы так, что каждому ребенку досталось одинаковое количество ручек и одинаковое количество карандашей. Какое наибольшее число учеников может быть в классе?
А) 2 Б) 19 В) 38 Г) 42
Галиулина В. Н.
Задача №6
Шестиугольную звезду согнули пополам (так, что две половинки совместились!), затем, еще раз пополам, снова совместив половинки. Какой результат мог получиться после того, как звезду развернули?
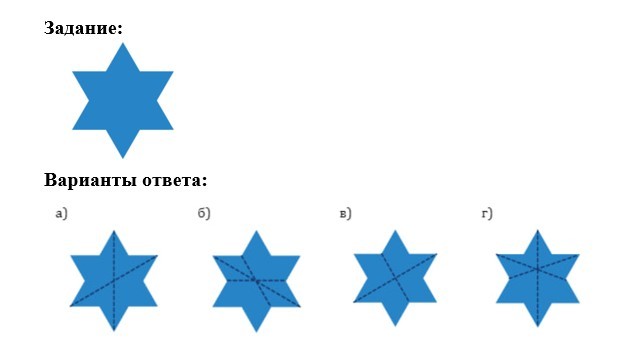
Галиулина В. Н.
Задача №7
Чебурашка почистил 3 апельсина и разломал каждый из них пополам. Затем каждую половинку он разломил на дольки. Всего у него получилось 35 долек. Сколько разломов он сделал?
А) 35 Б) 38 В) 34 Г) 32
Галиулина В. Н.
Задача №8
Когда старший брат ведёт младшего за руку, младший идет в два раза быстрее, чем сам по себе, а старший – в два раза медленней. Когда старший брат забирал младшего из детского сада, он вёл его за руку, но в конце пути младший брат захотел идти сам. И когда старший уже подошёл к дому, младшему оставалось ещё 24 метра. Сколько метров к этому моменту младший брат уже прошёл самостоятельно?
А) 6 м Б) 8 м В) 12 м Г) 24 м
Галиулина В. Н.
Задача №9
Из трехзначного числа отняли другое трехзначное число, полученное записью первого задом наперед (пример для двузначного числа: 74 – 47 = 27). Найдите наибольшее значение этой разности.
А) 891 Б) 792 В) 990 Г) 899
Галиулина В. Н.
Задача №10
Расставьте ёлочные украшения от самого лёгкого к самому тяжёлому.
А) Сушка, шарик, пирамидка, кубик Б) Шарик, сушка, кубик, пирамидка В) Кубик, шарик, сушка, пирамидка Г) Шарик, кубик, сушка, пирамидка
Галиулина В. Н.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Б | Г | В | В | В | В | Г | Б | Б | В |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



