Задания 1-го тура XVII олимпиады по математике для 6 класса
1 тур XVI1 олимпиады по математике прошел с 21 января по 9 февраля 2025 г.
Задачи олимпиады
Задача №1
Учитель задал Андрею и Ксении одинаковое домашнее задание. В понедельник каждый из них сделал первую треть задач самостоятельно. А во вторник они дорешали все оставшиеся задачи вместе (то есть дали на все эти задания одинаковые ответы). В четверг, когда учитель выдал им проверенные работы, оказалось, что у Андрея были правильно выполнены 68% всех задач, что он решал один, и 78% от общего количества заданных. У Ксении же оказались верны 86% от общего количества заданных. Какую часть задач Ксения сделала правильно одна?
А) 46 Б) 78 В) 88 Г) 92 Д) 94
Тодоров Е. И.
Задача №2
Во 2 «М» классе 27 учеников. У Васи, Коли и Пети по 3 друга среди одноклассников. При этом, у любых двух мальчиков из этих трех одноклассников есть хотя бы один общий друг. Какое наименьшее количество детей, которые не дружат ни с Васей, ни с Колей, ни с Петей, могут быть в классе?
А) 16 Б) 17 В) 18 Г) 19 Д) 20
Галиулина В. Н.
Задача №3
У нас в семье все люди простые: я заглядываю в учебник комбинаторики каждый третий день, мама каждый пятый, а папа — каждый седьмой. 31 декабря 2024 года так случилось, что мы смотрели в учебник все втроём. Сколько в 2025 году будет таких дней, в который хоть один из нас будет смотреть в учебник по комбинаторике?
А) 144 Б) 192 В) 195 Г) 198 Д) 246
Тодоров Е. И.
Задача №4
m, n, p — натуральные числа, для которых верно следующее равенство: Чему равно p?
А) 2 Б) 3 В) 4 Г) 6
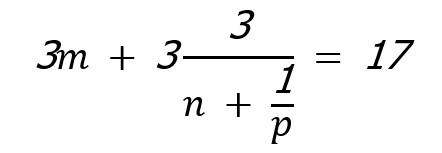
Миронов Д. Р.
Задача №5
В Зверином королевстве проходят соревнования по бегу. Коала Глеб каждый день пробегает целое количество километров, готовясь к соревнованиям ровно по часу в день. Три дня подряд Глеб старался бегать всё быстрее и быстрее, для этого он каждый день бежал с такой постоянной скоростью, что на преодоление километра ему требовалось некоторое целое количество минут, причём во второй день это количество было на 4 минуты меньше, чем в первый и на 4 минуты больше, чем в третий. Сколько километров пробежал Глеб за эти три дня подготовок?
А) 31 Б) 43 В) 45 Г) 46 Д) 51
Тодоров Е. И.
Задача №6
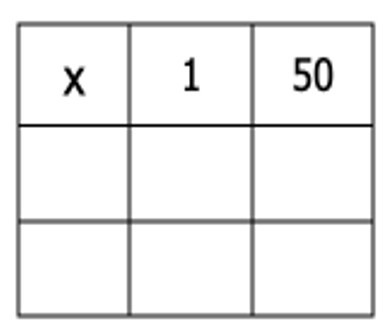
В квадрате 3 на 3 размещены все делители числа 100, причём так, чтобы произведения во всех столбцах, строках и диагоналях были равны. Какое число должно стоять на месте x?
А) 4 Б) 5 В) 10 Г) 20
Миронов Д. Р.
Задача №7
Чтобы впечатлить профессора, Крошка Цахес сложил 8 подряд идущих натуральных чисел и записал результат на доску. Однако профессор, даже будучи очарованным, сказал, что в вычислениях ошибка. Оказалось, что Крошка Цахес ошибся буквально на единицу. Какое число было записано на доске?
А) 33 Б) 44 В) 123 Г) 156
Галиулина В. Н.
Задача №8
Посмотрев мультфильм “Вверх”, Лёва решил поднять свою кошку Тасю в воздух при помощи воздушных шаров, наполненных гелием. Один шар может поднять 4 грамма, не считая собственного веса. Тася весит 5,28 кг. Цена одного шарика 19 рублей, наполнить его гелием стоит еще 150 рублей, но в связи с тем, что шариков надо много, продавец решил сделать скидку на услугу заполнение гелием - 15%. Сколько же рублей будет стоить Лёве обучить кошку летать?
А)200000 Б)134982 В)282345 Г)193380
Миронов Д. Р.
Задача №9
Петя, Витя и Катя играли друг с другом в крестики-нолики какое-то количество раз за день. К вечеру оказалось, что у Пети 2 победы, 2 поражения и 2 ничьи, у Вити 2 победы, 4 поражения и одна ничья. У Кати оказалось 1 поражение. А сколько побед у неё оказалось?
А) 1 Б) 2 В) 3 Г) 4 Д) невозможно определить
Тодоров Е. И.
Задача №10
Даня обозначил некоторые цифры буквами a и b, причём разные цифры были обозначены разными буквами, а одинаковые — одинаковыми. Оказалось, что после такой замены оказалось верным уравнение: a7b + 7ab + 6ab = 1bb7 (Например, за a7b обозначено не произведение, а трёхзначное число, в котором ровно a сотен, 7 десятков и b единиц.) Чему равно произведение a и b?
А) 15 Б) 20 В) 54 Г) 45
Миронов Д. Р.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Г | Б | Г | А | Г | Г | В | Г | В | Г |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



