Задания 1-го тура XVII олимпиады по математике для 7 класса
1 тур XVII олимпиады по математике прошел с 21 января по 9 февраля 2025 г.
Задачи олимпиады
Задача №1
Сколько решений в целых числах имеет уравнение? (y+1)(y2-y+1)=(2x)2
А) Уравнение не имеет решений в целых числах Б) 1 В) 2 Г) 3
Галиулина В. Н.
Задача №2
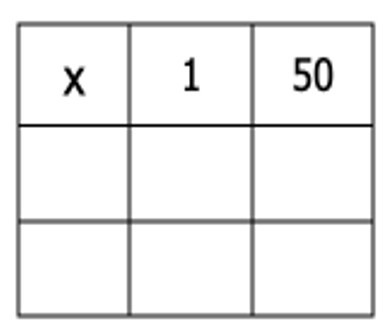
В квадрате 3 на 3 размещены все делители числа 100, причём так, чтобы произведения во всех столбцах, строках и диагоналях были равны. Какое число должно стоять на месте x?
А) 4 Б) 5 В) 10 Г) 20
Миронов Д. Р.
Задача №3
m, n, p — натуральные числа, для которых верно следующее равенство:
А) 2 Б) 3 В) 4 Г) 6
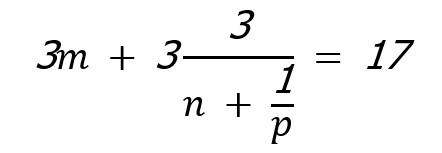
Миронов Д. Р.
Задача №4
Учитель задал Андрею и Ксении одинаковое домашнее задание. В понедельник каждый из них сделал первую треть задач самостоятельно. А во вторник они дорешали все оставшиеся задачи вместе (то есть дали на все эти задания одинаковые ответы). В четверг, когда учитель выдал им проверенные работы, оказалось, что у Андрея были правильно выполнены 68% всех задач, что он решал один, и 78% от общего количества заданных. У Ксении же оказались верны 86% от общего количества заданных. Какую часть задач Ксения сделала правильно одна?
А) 46 Б) 78 В) 88 Г) 92 Д) 94
Тодоров Е. И.
Задача №5
Про действительные числа x, y и z известно, что x*y*z<0 Какие значения принимает выражение?
А) -1, 0 и 1 Б) -2 и 2 В) -2, 0 и 2 Г) -1, 0, 1 и 2 Д) -2, -1, 0, 1 и 2
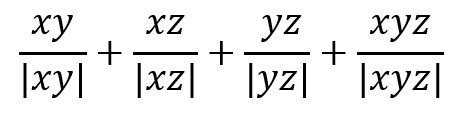
Тодоров Е. И.
Задача №6
В Зверином королевстве проходят соревнования по бегу. Коала Глеб каждый день пробегает целое количество километров, готовясь к соревнованиям ровно по часу в день. Три дня подряд Глеб старался бегать всё быстрее и быстрее, для этого он каждый день бежал с такой постоянной скоростью, что на преодоление километра ему требовалось некоторое целое количество минут, причём во второй день это количество было на 4 минуты меньше, чем в первый и на 4 минуты больше, чем в третий. Сколько километров пробежал Глеб за эти три дня подготовок?
А) 31 Б) 43 В) 45 Г) 46 Д) 51
Тодоров Е. И.
Задача №7
В турнире по настольному теннису игроки встречались парами и играли на вылет (каждый проигравший выбывал из турнира). В конце турнира оказалось, что людей, которые проиграли больше матчей, чем выиграли, на 16 больше, чем тех, кто выиграл больше матчей, чем проиграл. Сколько всего людей участвовало в турнире?
А) 32 Б) 48 В) 64 Г) 96
Тодоров Е. И.
Задача №8
Сумма тридцати последовательных натуральных чисел равна 2025. Чему равно наибольшее из них?
А) 79 Б) 81 В) 82 Г) 83
Тодоров Е. И.
Задача №9
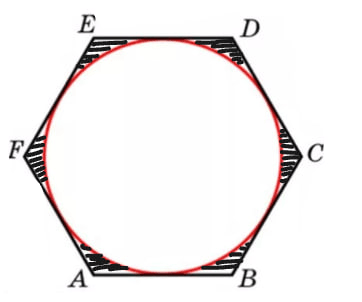
Радиус окружности, вписанной в правильный шестиугольник равен 5 см. Площадь некоторого равностороннего треугольника, одна сторона которого равна стороне АВ - 16 см^2. Чему равна площадь заштрихованной части?
(А) 2 (Б) 3 (В) 4 (Г) 5 (Д) 8
Миронов Д. Р.
Задача №10
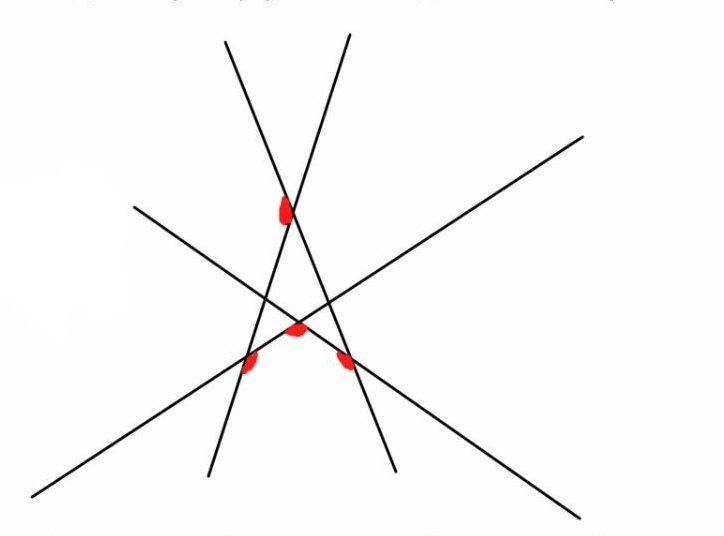
Найдите сумму углов, выделенных красным на рисунке:
А) 540 Б) 570 В) 600 Г) 720
Миронов Д. Р.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | А | Г | А | Г | Б | Г | В | В | В | А |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


