Задания 2-го тура XVII олимпиады по математике для 5 класса
2 тур XVII олимпиады по математике прошел 2 марта 2025 г.
Задачи олимпиады
Задача №1
Четыре компьютера А, Б, В и Г сломались, поэтому когда в них вводишь какое-то число, каждый компьютер умножает его на какое-то своё число (фиксированное и уникальное для каждого компьютера), после чего выводит на экран сразу результат умножения. Даня загадал четыре числа и ввёл их в компьютеры: первое число — в А, второе — в Б, третье — в В, а четвёртое — в Г. На экранах загорелись ответы 16, 35, 66, 30 (в том же порядке, в котором были введены числа). Потом Даня взял загаданные числа в том же порядке и ввёл их в другие компьютеры: первое число — в Г, второе — в А, третье — в Б, а четвёртое — в В. На экранах загорелись ответы 24, 14, 55, 60 (в том же порядке, в котором были введены числа). Какие числа и в каком порядке загадал Даня?
Тодоров Е. И.
Задача №2
Перед вами 9 колбочек с жидкостями. В каждой колбе изначально разное количество жидкости: 2л, 4л, 1л, 5л, 6л, 9л, 8л, 7л, и 3л. За один ход можно выбрать две любые колбочки и перелить из них одинаковое количество жидкости в какую-то третью (Например, можно выбрать 1 и 2 колбочки и перелить по 1л в третью). Можно ли за 4 таких хода сделать так, чтобы во всех колбочках оказалось поровну жидкости? Если можно, приведите пример.
Санкеева О. О.
Задача №3
Барон Мюнхгаузен рассказал, что видел в пустыне Сахара 12 кактусов высотой от 1 до 12 метров, стоявших по кругу. Напротив кактуса высотой 12 метров стоял кактус высотой 11 метров. Трехметровый и метровый кактусы стояли рядом. При этом барон насчитал ровно восемь кактусов, у которых разница в высоте с левым и правым «соседом» была одинаковая. Могло ли такое быть?
Галиулина В. Н.
Задача №4
Сколько двухзначных чисел обладают следующим свойством: "Если данное число сложить с числом, полученным из данного перестановкой цифр, мы получим результат 143"?
Тодоров Е. И.
Задача №5
В трёх пробирках лежат шарики: на самом дне первой лежит синий, а сверху два красных, во второй пробирке то же самое, а в третьей только два синих шарика. Размеры шариков и пробирок таковы, что в пробирку помещается только один шарик по ширине и только четыре по высоте. За одно действие можно достать верхний шарик из какой-то пробирки и переложить в какую-то другую, если в той есть место. За какое наименьшее количество действий можно добиться того, чтобы в первой пробирке остались только красные шарики, а в третьей — только синие?
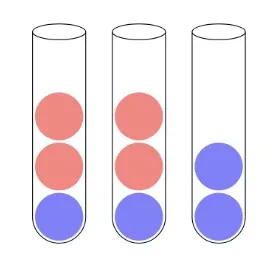
Тодоров Е. И.
Задача №6
У Кости был блокнот, на страницах которого не было номеров. Костя пронумеровал страницы, начиная с первой, на которой он написал “1”. Когда он подписал номер на последней странице, он посчитал, что всего он написал 278 цифр. Докажите, что Костя ошибся в подсчётах.
Тодоров Е. И.
Задача №7
Рассеянный с улицы Бассейной вышел из вагона метро на станции Московская и поехал вверх по эскалатору, стоя на месте. Но на середине эскалатора он вдруг, вспомнил, что его квартира находится у станции Парк Победы, и со всех ног помчался по этому же эскалатору вниз. Сколько (полных) ступеней на видимой части эскалатора, если Рассеянный пробежал 84 ступени, и путь вниз занял у него вдвое меньше времени, чем путь наверх?
Галиулина В. Н.
Задача №8
В ряд расположены 15 коробок. В каждой коробке либо пусто, либо лежит подарок. Хитрый Лев знает, что среди пяти подряд идущих коробок всегда ровно две будут с подарком, а еще что пустые коробки идут по три подряд. Как Льву гарантированно найти все подарки, открыв не более семи коробок?
Галиулина В. Н.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


