Задания 2-го тура XV олимпиады по математике для 5 класса

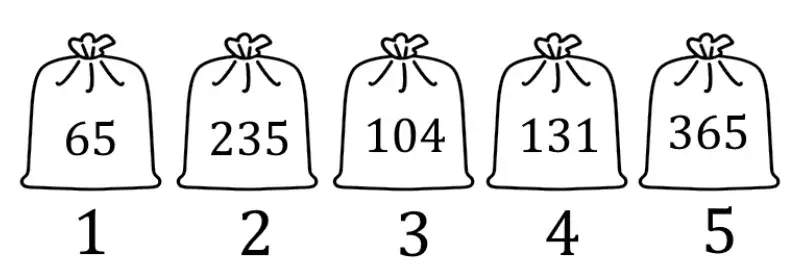
У Аркаши-фокусника есть 600 белых шариков и 1200 чёрных. Он разложил их по пяти мешкам (в каждом лежат только белые или только чёрные шарики). Теперь он хочет достать один белый шарик с первой попытки. Как ему это сделать? Вес мешков указан на картинке. Все шарики весят одинаково.

Биолог Селезнёв изучает колонии марсианских одноклеточных водорослей. В отличие от земных, одна клетка может разделиться только на 11 или 21 клетку за раз. Он поместил одну клетку в агар(питательный раствор) и, спустя сутки, примерно подсчитал, что в колонии не менее 1170, но не более 1200 одноклеточных. Какое количество водорослей могут быть в колонии? Назовите все возможные варианты ответов.

На доске написано 100 попарно различных натуральных чисел, каждое из которых не превышает 1000. В мешочке лежат 1200 карточек со знаком «-» и 250 карточек со знаком «+». Каждый ход Вася наугад достает карточку из мешочка. Если попался минус, то из каждого числа он вычитает 1. Если попался плюс, то к каждому числу он прибавляет 1. Докажите, что в какой-то момент ровно половина чисел окажутся положительными.

Существуют ли 5 дробей (не обязательно правильных!) таких, что произведение всех пяти дробей равно целому числу, но если выбрать некоторые из них (но не все), то их произведение не будет целым?

Чтобы как-то отличать своих личинок, пчелы пронумеровали их от 1 до 19. Могут ли они разместить личинок в сотах так, чтобы разность никаких номеров двух соседних личинок не делилась на 3?

Если справа от суммы цифр двузначного числа N приписать произведение его цифр, то результат будет равняться исходному числу N. Найдите все такие числа и докажите, что других нет.

Вокруг большой лужи встали 20 жителей острова рыцарей и лжецов (рыцари всегда говорят правду, лжецы всегда лгут) и посмотрели на неё. Потом каждый из 20 людей грустно сказал: «Среди следующих трёх людей справа от меня по кругу есть хотя бы 2 рыцаря». Сколько среди них было рыцарей?