Задания 1-го тура XVI олимпиады по математике для 5 класса

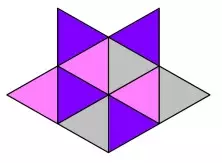
Сосчитайте сколько четырёхугольников в этой фигуре?

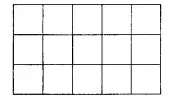
Фигуру, изображенную ниже, разрезали на 5 различных по площади прямоугольников по линиям сетки. Шаг сетки считать равным 1*1. Чему равен периметр прямоугольника с наибольшей площадью?

Путник поднимается в гору по лестнице, в которой 2024 ступеньки. Как правило, он шагает через ступеньку, но после десяти таких шагов он отдыхает и делает 4 шага, не перешагивая ни одной ступеньки. Сколько шагов сделал путник?

После того, как из числителя некоторой дроби вычли 239, а к знаменателю прибавили 239, получилась дробь, значение которой равно 1/7. Какой была исходная дробь, если известно, что сумма её числителя и знаменателя была равна 880?

В четыре бокала налит виноградный сок. Первый и второй бокал заполнен на 3/4, третий — на 5/6, 4-й — на 1/3. Золушка решила сделать так, чтобы всем гостям сока досталось поровну. За один раз она может перелить сок из одного бокала в другой так, чтобы второй бокал оказался заполнен до краев, либо так, чтобы сока в бокалах стало поровну. За какое минимальное количество шагов она может это сделать?

Семья циркачей несколько дней подряд исполняет номер «Башенка». Для этого члены семейства встают на плечи друг к другу в один или несколько рядов так, чтобы в любом ряду ниже было не меньше человек, чем в ряду выше. Сколько дней подряд циркачи могут составлять «Башенки» из 6 человек, не повторяясь, если в «Башенке» должен быть хотя бы один ряд

Среди высказываний ниже лишь одно истинно. Выберете верный ответ на эту задачу:

На бал пришли 4 дамы и 4 кавалера. Камердинер хочет запускать гостей внутрь таким образом, чтобы любая дама могла найти кавалера для танца, как только она зайдёт в зал. Для этого камердинер просит дам и кавалеров выстроиться в очередь. Сколькими способами он может составить такую очередь? (варианты, в которых местами меняются только несколько кавалеров или только несколько дам, считать одинаковыми)

Рыцари всегда говорят правду, а лжецы всегда лгут. Однажды за круглый стол усадили 89 рыцарей и лжецов. Каждый из них осмотрелся и сказал: «Оба моих соседа – лжецы!» Какое наибольшее и наименьшее количество рыцарей могло быть среди них? В ответ запишите разность между этими числами.

Числа зашифрованы словами КУЛАК, КУЛИК, ЛАК и ЛИК. Одинаковыми буквами обозначены одинаковые цифры, разными — разные. Известно, что ровно одно из этих чисел больше 10290, и ровно одно из них меньше 240. Найдите, чему равно А + И. Варианты ответа: