Задания 2-го тура XVI олимпиады по математике для 5 класса
2 тур XVI олимпиады по математике прошел 27 октября 2024 года
Задачи олимпиады
Задача №1
Какую максимальную сумму можно получить, решив ребус ПИОН + ПОНИ (Каждой букве соответствует определенная цифра. Разным буквам разные цифры.)
Миронов Д. Р.
Задача №2
Все сосуды имеют одинаковую форму, но разную высоту. Посередине каждого сосуда есть трубочка, соединённая с верхом следующего по величине сосуда. Сколько нужно залить воды в самый большой сосуд, чтобы самый маленький наполнился до краёв, если второй сосуд слева вмещает 48 миллилитров?

Галиулина В. Н.
Задача №3
Девочки Маша и Даша придумали два различных четырёхзначных числа, которые делятся на 9. Оказалось, что у обоих чисел первая цифра – двойка, вторая цифра – тройка, и четвёртые цифры тоже совпадают. Перечислите все возможные пары таких чисел и объясните, почему других нет.

Бородинова Е. А.
Задача №4
Есть трёхзначное число. Катя, Рома, Саша и Женя сказали про него: Катя: число оканчивается цифрой 5 и число начинается с чётной цифры Рома: число не делится на 10, и если его умножить на 2, оно не будет делиться на 5 Саша: число в 4 раза больше суммы своих цифр и число делится на 15 Женя: у числа последние две цифры одинаковые и первая цифра 2 Оказалось, что каждый человек ровно один раз соврал и ровно один раз сказал правду. Что же это за число?
Бородинова Е. А.
Задача №5
Лосяш и Пин играют в игру: Лосяш выписывает на доску такую цифру от 1 до 9, чтобы сумма двух последних цифр на доске делилась на 9. Пин же выписывает такую цифру, чтобы сумма двух последних цифр делилась на 10. Какая цифра будет выписана на 1001-м ходу, если первый ходит Лосяш, и до начала игры на доске была написана единственная цифра 5?

Галиулина В. Н.
Задача №6
Башня составлена из магнитных кубиков, как показано на рисунке. Башню окунули в красную краску, а потом разобрали на кубики. Сколько кубиков будут покрашены ровно с трех сторон?
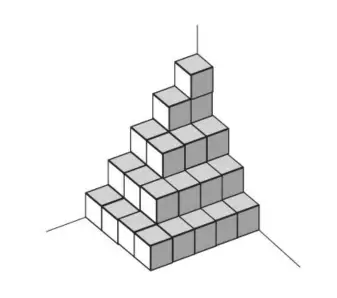
Галиулина В. Н.
Задача №7
Перед вами 9 колбочек с жидкостями. В каждой колбе изначально разное количество жидкости: 2л, 4л,1л, 5л, 6л, 9л, 8л, 7л, и 3л. За один ход можно выбрать две любые колбочки и перелить из них одинаковое количество жидкости в какую-то третью (Например, можно выбрать 1 и 2 колбочки и перелить по 1л в третью). Размеры колб такие, что могут вместить жидкость из всех сосудов. Можно ли за 5 таких ходов перелить все жидкости в одну колбу? Если можно, приведите пример.
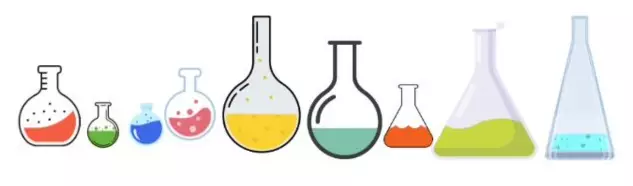
Санкеева О. О.
Задача №8
Алексиос попал в ловушку Сфинкса, чтобы пройти мимо, придется обыграть его в его игре: есть полоска 2х20, игроки по очереди заполняют ее фигурками. Сфинкс ставит квадратики 2х2, а Алексиос -- трёхклеточные уголки, которые можно поворачивать и переворачивать. Сфинкс ходит вторым, проигрывает тот, кто не может сделать ход. Придумайте как Алексиосу победить в любом случае, как бы ни ходил мудрый Сфинкс.
Галиулина В. Н.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



