Задания 1-го тура XV олимпиады по математике для 5 класса
1 тур XV олимпиады по математике прошел с 15 января по 6 февраля 2024 года
Задачи олимпиады
Задача №1
Среди учеников 4-го «М» класса каждый был либо на экскурсии, либо в театре, либо в походе. Все, кто был в театре, после спектакля пошли на экскурсию. Тех, кто не был в походе, меньше, чем тех, кто не был на экскурсии. На каком мероприятии было больше всего детей?
(А) на экскурсии (Б) в театре (В) в походе (Г) невозможно определить
Галиулина В. Н.
Задача №2
Сколько ниточек между алмазами нужно разрезать, чтобы большое алмазное колье с картинки превратилось в алмазную нить, если все бусины из колье должны оказаться нанизанными на нить? Например, в колье из четырех бусин пришлось бы отрезать всего одну ниточку, как показано ниже.
(А) 8 (Б) 9 (В) 10 (Г) 11 (Д) 12
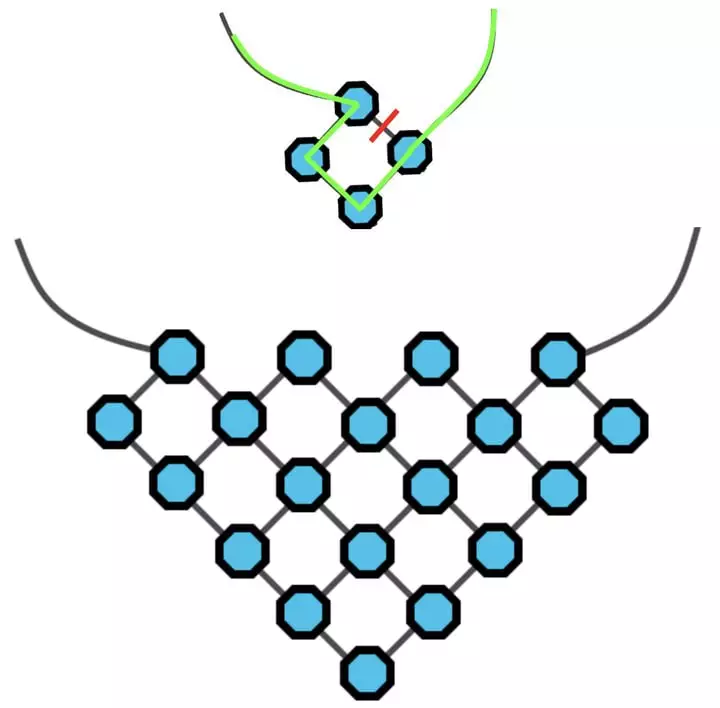
Галиулина В. Н.
Задача №3
Чтобы впечатлить профессора Крошка Цахес сложил восемь подряд идущих чисел и записал результат на доску. Однако профессор сказал, что в вычислениях ошибка. Оказалось, что Крошка Цахес ошибся буквально на единицу. Какое число могло быть записано на доске?
(А) 52 (Б) 44 (В) 123 (Г) 156
Галиулина В. Н.
Задача №4
Вася нашел наименьшее натуральное число, произведение цифр которого равняется 72, и вычел из него сумму его цифр. Какой результат он получил?
(А) 72 (Б) 81 (В) 234 (Г) 252 (Д) среди вышеперечисленных нет правильного ответа
Галиулина В. Н.
Задача №5
В городе N построили необычную беговую дорожку. Два спортсмена стартуют одновременно из точки А (середины синей дорожки), бегут в противоположных направлениях с одинаковыми скоростями. На развилках они могут поворачивать куда угодно, только не в обратном направлении. Каждый спортсмен пробежал по 2 километра. Чему равно наибольшее количество раз, которое они могли встретиться, не считая встречу на старте, если за всю тренировку они ни разу не бежали рядом?
(А) 16 (Б) 15 (В) 17 (Г) 6 (Д) 7
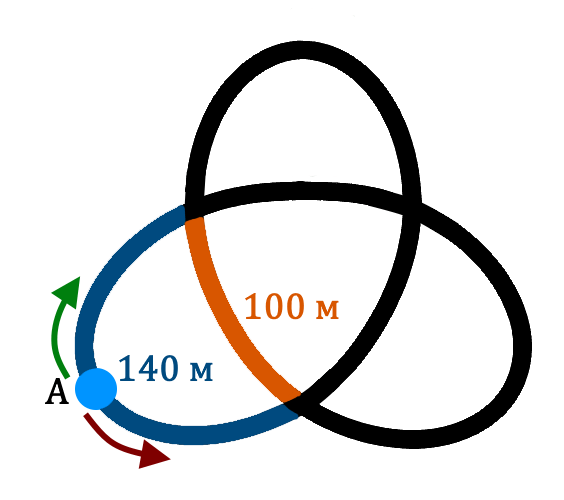
Галиулина В. Н.
Задача №6
На отрезке AD длиной 33 сантиметров стоят точки B и C так, что: точки расположены в порядке ABCD; отрезок BC в два раза длиннее отрезка AB; а отрезок CD — в 4 раза длиннее BC. Найдите длину отрезка AC
(А) 8 (Б) 9 (В) 12 (Г) 18
Галиулина В. Н.
Задача №7
15 шоколадок тяжелее 19-ти ирисок, но 3 шоколадки легче 4-х ирисок. Когда на одну чашу весов положили 9 ирисок, а на другую – несколько шоколадок, весы оказались в равновесии. Сколько шоколадок положили на весы?
(А) 5 (Б) 6 (В) 7 (Г) 8
Галиулина В. Н.
Задача №8
Маленькая обезьянка съедает все фрукты с дерева за 6 часов, а ее мама и папа (каждый по отдельности) съедают в два раза быстрее. За сколько времени семья обезьянок вместе съест все фрукты с дерева?
(А) 52 минуты (Б) 1 час 12 минут (В) 1 час 36 минут (Г) 1 час 44 минуты (Д) 2 часа 8 минут
Галиулина В. Н.
Задача №9
На сколько квадратов (не обязательно одинаковых) нельзя разрезать квадрат?
(А) 4 (Б) 5 (В) 6 (Г) 7 (Д) правильных ответов несколько
Галиулина В. Н.
Задача №10
На космической станции работают три друга: биолог, инженер и астрофизик. Их фамилии Шепард, Хокинг и Купер. У инженера нет ни братьев, ни сестер. Он самый младший из друзей. Купер, женатый на сестре Шепарда, старше биолога. Назовите фамилии биолога, инженера и астрофизика (именно в этом порядке).
(А) Шепард, Хокинг, Купер (Б) Хокинг, Купер, Шепард (В) Хокинг, Шепард, Купер (Г) Шепард, Купер, Хокинг
Галиулина В. Н.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | В | В | В | А | А | Б | В | Б | Б | А |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


