Задания 2-го тура XVII олимпиады по математике для 6 класса
2 тур XVI1 олимпиады по математике прошел 2 марта 2025 г.
Задачи олимпиады
Задача №1
Известно, что 5 прямых расположенных на плоскости не могут пересекаться больше, чем в 10 точках. А сколько точек пересечения у 5 прямых быть не может? Приведите все варианты меньшие 10 и докажите, что других нет.
Иванюк Д. В.
Задача №2
Четыре компьютера А, Б, В и Г сломались, поэтому когда в них вводишь какое-то число, каждый компьютер умножает его на какое-то своё число (фиксированное и уникальное для каждого компьютера), после чего выводит на экран сразу результат умножения. Даня загадал четыре числа и ввёл их в компьютеры: первое число — в А, второе — в Б, третье — в В, а четвёртое — в Г. На экранах загорелись ответы 16, 35, 66, 30 (в том же порядке, в котором были введены числа). Потом Даня взял загаданные числа в том же порядке и ввёл их в другие компьютеры: первое число — в Г, второе — в А, третье — в Б, а четвёртое — в В. На экранах загорелись ответы 24, 14, 55, 60 (в том же порядке, в котором были введены числа). Какие числа и в каком порядке загадал Даня?
Тодоров Е. И.
Задача №3
Квадрат на рисунке ниже разбит на четыре прямоугольника с одинаковой площадью. Короткая сторона верхнего прямоугольника равна 6. Чему равна площадь квадрата?
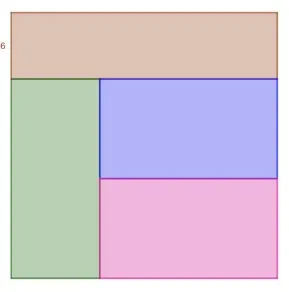
Тодоров Е. И.
Задача №4
Кенгурёнок Ваня каждый день пробегает натуральное количество километров, готовясь к соревнованиям ровно по часу в день. Три дня подряд Ваня старался бегать всё быстрее и быстрее, для этого он каждый день бежал с такой постоянной скоростью, что на преодоление каждого километра ему требовалось некоторое натуральное количество минут. Будем называть это количество минут темпом бега Вани. Оказалось, что темп Вани каждый день уменьшался на одинаковое количество минут каждый день. Сколько километров пробежал Ваня за эти три дня подготовок?
Тодоров Е. И.
Задача №5
Натуральные числа от 1 до 20 выписали в строчку в некотором порядке. Потом каждое число сложили с его номером в строчке (первое число в строчке сложили с 1, второе сложили с 2, ..., последнее сложили с 20). Могли ли у всех полученных сумм оказаться разные остатки при делении на 20?
Тодоров Е. И.
Задача №6
Петя и Вася играют в игру. Изначально на доске написано число 1. За один ход разрешается к написанному на доске числу прибавить 20 или умножить его на 25, старое число стереть и вместо него написать результат своих вычислений. Побеждает тот, после чьего хода на доске впервые окажется число 2025 или больше. Первым ходит Петя. У кого из игроков есть выигрышная стратегия и какая она?
Тодоров Е. И.
Задача №7
В трёх пробирках лежат шарики: на самом дне первой лежит синий, а сверху два красных, во второй пробирке то же самое, а в третьей только два синих шарика. Размеры шариков и пробирок таковы, что в пробирку помещается только один шарик по ширине и только четыре по высоте. За одно действие можно достать верхний шарик из какой-то пробирки и переложить в какие-то другую, если в той есть место. За какое наименьшее количество действий можно добиться того, чтобы в первой пробирке оказались все красные шарики, а в третьей — все синие?
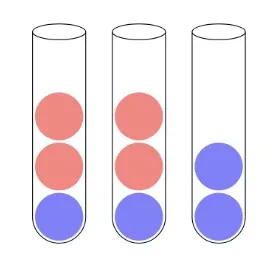
Тодоров Е. И.
Задача №8
Гадалка Ариана придумывает новый способ предсказания судьбы с помощью карт. Для этого она выкладывает 16 карт на стол, сложив их в одну стопку. Потом Ариана берёт со стола одну стопку, в которой больше одной карты, и разбивает на две стопки поменьше, которые тоже кладёт на стол. После этого Ариана считает карты в этих двух новых стопках, перемножает их количества, а произведение записывает в волшебную книгу, чтобы потом истолковать их, согласно правилам численной магии. (Например, если первым ходом Ариана разделит карты на две стопки в 6 и 10 карт, первой записью в книге станет число 60.) Ариана продолжает такие свои действия до тех пор, пока на столе не останутся только стопки по одной карте. Чему может быть равна сумма всех чисел, записанных в книге Арианы в конце такого гадания?
Тодоров Е. И.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



