Задания 2-го тура XVI олимпиады по математике для 6 класса
1 тур XVI олимпиады по математике прошел с 27 октября 2024 года.
Задачи олимпиады
Задача №1
Девочки Маша и Даша придумали два различных четырёхзначных числа, которые делятся на 9. Оказалось, что у обоих чисел первая цифра – двойка, вторая цифра – тройка, и последние цифры тоже совпадают. Перечислите все возможные пары таких чисел и объясните, почему других нет.

Бородинова Е. А.
Задача №2
Шайбу запускают из угла поля величиной 70x70 метров. Она скользит по льду (не снижая скорости), и после удара о стенку на расстоянии 30 метров от угла поля (см. картинку) отскакивает (всегда) под тем же углом и с той же скоростью. Через сколько отскоков шайба вновь окажется в углу?
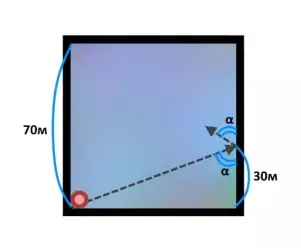
Галиулина В. Н.
Задача №3
1 января в некотором банке планируется взять кредит в размере 1 млн. рубле на три года на следующих условиях: в конце каждого года (31 декабря в 23:58) остаток текущего долга возрастает на 25%, а уже 31 декабря в 23:59 нужно погасить часть долга. Все платежи по кредиту одинаковы. Всего их 3, по одному в год. Какой должен быть платеж по кредиту, чтобы долг был погашен в срок?
Миронов Д. Р.
Задача №4
Леонардо Ф. хочет замостить дорожку перед своим домиком в городе П. Для этого у него есть плитки размером 50x100 сантиметров. Известно, что дорожка прямая, имеет длину 4 метра и ширину 1 метр. Сколькими способами Леонардо может замостить дорожку, если плитки нельзя резать на части?

Тодоров Е. И.
Задача №5
Есть трёхзначное число. Катя, Рома, Саша и Женя сказали про него: Катя: число оканчивается цифрой 5 и число начинается с чётной цифры Рома: число не делится на 10, и если его умножить на 2, оно не будет делиться на 5 Саша: число в 4 раза больше суммы своих цифр и число делится на 15 Женя: у числа последние две цифры одинаковые и первая цифра 2 Оказалось, что каждый человек ровно один раз соврал и ровно один раз сказал правду. Что же это за число?

Бородинова Е. А.
Задача №6
Перед вами 9 колбочек с жидкостями. В каждой колбе изначально разное количество жидкости: 2л, 4л,1л, 5л, 6л, 9л, 8л, 7л, и 3л. За один ход можно выбрать две любые колбочки и перелить из них одинаковое количество жидкости в какую-то третью (Например, можно выбрать 1 и 2 колбочки и перелить по 1л в третью). Размеры колб такие, что могут вместить жидкость из всех сосудов. Можно ли за 5 таких ходов перелить все жидкости в одну колбу? Если можно, приведите пример.
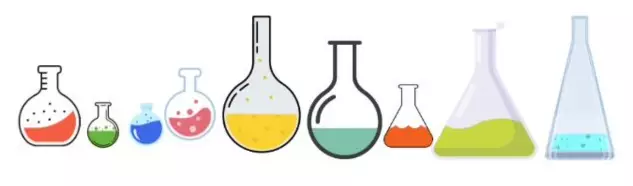
Санкеева О. О.
Задача №7
Алексиос попал в ловушку Сфинкса, чтобы пройти мимо, придется обыграть его в его игре: есть полоска 2х20 игроки по очереди заполняют ее фигурками. Сфинкс ставит квадратики 2х2, а Алексиос - трёхклеточные уголки, которые можно поворачивать и переворачивать. Сфинкс ходит вторым, проигрывает тот, кто не может сделать ход. Придумайте как Алексиосу победить в любом случае, как бы ни ходил мудрый Сфинкс.
Галиулина В. Н.
Задача №8
В некотором месте учатся пять хвастливых математиков. Однажды каждого из них спросили про успехи их коллег в олимпиадах. Известно, что каждый хвастливый математик преуменьшает заслуги других, чтобы самому казаться лучше, то есть любой математик возьмёт реальное количество олимпиад, в которых победил его коллега, и вычтет из этого количества своё любимое число. Любимое число у каждого математика может отличаться от любимых чисел коллег, но любить своё число он будет всю жизнь. Однажды этим математикам задали вопрос: "Сколько олимпиад выиграл этот твой коллега?" - причём оказалось, что вопрос этот задали каждому и про каждого (кого-то одного) по одному разу. Последовали ответы: 7, 5, 8, 10, 6. А потом им снова задали этот же вопрос, но уже указали на других коллег, хотя снова оказалось, что спросили у каждого и про каждого по одному разу. Первые четверо дали ответы 6, 4, 7, 11. Что мог ответить пятый?
Тодоров Е. И.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


