Задания 2-го тура XVII олимпиады по математике для 7 класса
2 тур XVII олимпиады по математике прошел 2 марта 2025 г.
Задачи олимпиады
Задача №1
Известно, что 5 прямых расположенных на плоскости не могут пересекаться больше, чем в 10 точках. А сколько точек пересечения у 5 прямых быть не может? Приведите все варианты меньшие 10 и докажите, что других нет.
Иванюк Д. В.
Задача №2
В треугольнике два внутренних угла относятся как 1:4. Про третий угол известно, что он на 24° больше самого меньшего угла. Найдите все внутренние углы треугольника.
Ерина Ю. Ю.
Задача №3
Найдите все пары натуральных чисел x и y, являющихся решениями уравнения xy + 4y - 7x = 47
Тодоров Е. И.
Задача №4
Натуральные числа от 1 до 20 выписали в строчку в некотором порядке. Потом каждое число сложили с его номером в строчке (первое число в строчке сложили с 1, второе сложили с 2, ..., последнее сложили с 20). Могли ли у всех полученных сумм оказаться разные остатки при делении на 20?
Тодоров Е. И.
Задача №5
Гадалка Ариана придумывает новый способ предсказания судьбы с помощью карт. Для этого она выкладывает 16 карт на стол, сложив их в одну стопку. Потом Ариана берёт со стола одну стопку, в которой больше одной карты, и разбивает на две стопки поменьше, которые тоже кладёт на стол. После этого Ариана считает карты в этих двух новых стопках, перемножает их количества, а произведение записывает в волшебную книгу, чтобы потом истолковать их, согласно правилам численной магии. (Например, если первым ходом Ариана разделит карты на две стопки в 6 и 10 карт, первой записью в книге станет число 60.) Ариана продолжает такие свои действия до тех пор, пока на столе не останутся только стопки по одной карте. Чему может быть равна сумма всех чисел, записанных в книге Арианы в конце такого гадания?
Тодоров Е. И.
Задача №6
Кенгурёнок Ваня каждый день пробегает натуральное количество километров, готовясь к соревнованиям ровно по часу в день. Три дня подряд Ваня старался бегать всё быстрее и быстрее, для этого он каждый день бежал с такой постоянной скоростью, что на преодоление каждого километра ему требовалось некоторое натуральное количество минут. Будем называть это количество минут темпом бега Вани. Оказалось, что темп Вани каждый день уменьшался на одинаковое количество минут каждый день. Сколько километров пробежал Ваня за эти три дня подготовок?
Тодоров Е. И.
Задача №7
Лиза нарисовала на клетчатом поле красную фигурку (см. рисунок). Какое минимальное количество клеточек Лиза должна добавить к своей фигурке, чтобы её можно было разрезать на S-тетрамино (так называются фигурки, нарисованные синим справа)?
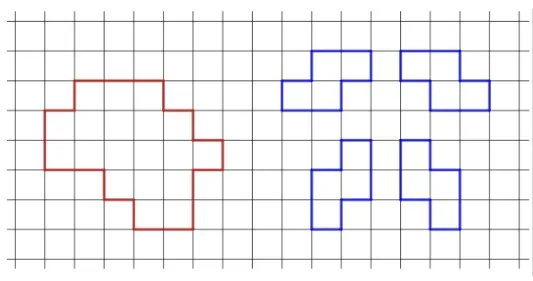
Тодоров Е. И.
Задача №8
В пирамиде, изображенной на рисунке каждая ячейка над нижней строкой содержит сумму чисел в двух ячейках под ней. Сумма чисел в нижней строке равна 17. Найдите какое число закрыто знаком вопроса.
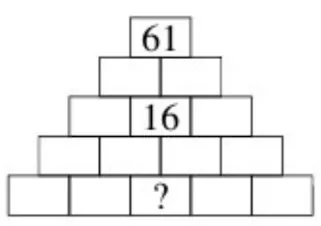
Галиулина В. Н.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


