Задания 1-го тура XVIII олимпиады по математике для 5 класса
1 тур XVIII олимпиады по математике прошел с 16 по 29 июня 2025 г.
Задачи олимпиады
Задача №1
Три подруги: Света, Настя и Наташа, живут на одной улице. Их профессии — доктор, инженер и музыкант. У младшей — доктора, нет брата. Наташа старше инженера и замужем за братом Насти. Назовите имена врача и инженера (именно в таком порядке).
А) Света и Настя Б) Настя и Наташа В) Наташа и Настя Г) Света и Наташа
Галиулина В.Н.
Задача №2
У фермера Максима есть загон для скота в форме правильного шестиугольника. Ему нужно покрасить все 6 столбов в углах загона. У него есть краски трех цветов, но каждого цвета ему хватит не больше, чем на 2 столба. При этом Максим хочет, чтобы получившаяся раскраска столбов была симметрична относительно какой-то прямой. Сколькими способами Максим может раскрасить столбы загона?
А) 30 Б) 36 В) 18 Г) 15
Булавинов Б.А.
Задача №3
Мама дала Катеньке несколько монеток по 2 и 5 рублей, причём точно были и такие, и такие. Сколькими различными способами мама могла так дать монетки Катеньке, чтобы пятирублёвых монеток было не больше, чем двухрублёвых, и чтобы все эти монетки вместе стоили 42 рубля?
А) 1 Б) 2 В) 3 Г) 4
Тодоров Е.И.
Задача №4
У Лизы есть очень тонкий лист бумаги размером 20х30 см. Она многократно складывает его пополам вдоль более короткой стороны. Она прекращает складывать, когда у нее остается прямоугольник площадью 75 см². Каков периметр конечного прямоугольника?
A) 35 Б) 65 В) 15 Г) 70
Галиулина В.Н.
Задача №5
В детском саду Ромашка меньше 500 воспитанников. Пятая часть от всех ребят сегодня не съела суп на обед, четверть — не выпила компот, треть — отказалась от котлеты, а одна седьмая — отдала кусочек хлеба соседу. Сколько ребят не выпили компот?
А) 105 Б) 120 В) 126 Г) 210
Галиулина В.Н.
Задача №6
Пять девушек бежали наперегонки. Первой начала Оля, за ней Катя, затем Амина, затем Соня и, наконец, Маша. Всякий раз, когда девушка обгоняла другую девушку, ей начислялся 1 балл. Соня финишировала первой, затем Катя, затем Оля, затем Маша и, наконец, Амина. Какое наименьшее общее количество баллов можно было бы получить?
A) 9 Б) 8 В) 6 Г) 5
Галиулина В.Н.
Задача №7
Лизе очень скучно, поэтому она делает с числом n одно из следующих действий: – если n<5, Лиза умножает его на 4 – если число n>=5 и чётное, Лиза делит его на 2 – если число n>=5 и нечётное, Лиза прибавляет к нему 3 Что получится, если Лиза применит 2025 таких действий к числу 7?
А) 4 Б) 5 В) 8 Г) 16
Тодоров Е.И.
Задача №8
На рисунке показана фигура «почтикуб». Как могла бы выглядеть развёртка «почтикуба»?
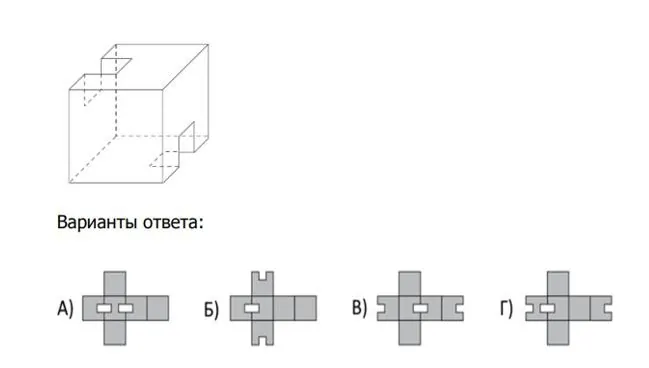
Галиулина В.Н.
Задача №9
Чтобы приготовить 7 тысяч литров бетона необходимо потратить 2114 кг цемента. Сколько фургонов надо заказать, чтобы перевезти цемент, необходимый для приготовления 16 кубических метров бетона, если один фургон выдерживает не более 1 тонны груза?
А) 3 Б) 4 В) 5 Г) 6
Ерина Ю.Ю
Задача №10
С числом n n, написанным на доске, за один ход можно проделывать две операции: либо прибавить к нему 202, либо умножить его на 5. Петя и Вася играт в игру, в которой они по очереди применяют операции к числу на доске, после чего старое число стирается, и на его место записывается результат примерения операции (например, можно стереть число 1 и написать вместо него 203 или 5). Побеждает тот, кто первым получит число 2025 или больше. Игроки ходят по очереди, начинает Петя. При каком наибольшем n n Петя гарантированно может выиграть ровно за два хода?
А) 196 Б) 202 В) 225 Г) 405
Тодоров Е.И.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | А | Б | В | А | А | Г | В | В | В | Б |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


