Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 3 класс

На данной странице размещены олимпиадные задания с решением для 3 класса.
Олимпиада по математике прошла с 15 сентября по 2 октября 2022 года

Посмотреть ответы на все задания олимпиады

Посмотреть ответы на задания

Вопрос №	1	2	3	4	5	6	7	8	9	10	11	12	13
Ответ	Г	В	Д	Д	Б	Д	Г	Б	В	А	Б	А	В

Задача №1
Сколько надземных этажей в многоэтажном доме, если Алина живет на 7 этаже сверху и на 8 этаже снизу с учетом трёх подземных этажей?
(A) 15
(Б) 14
(В) 12
(Г) 11
(Д) 9

Задача №2
Следующий год 2023. Через сколько лет будет ближайший год с такой же суммой цифр, и в записи которого будут использованы только 0,1, 2 и 3?
(A) 3103
(Б) 2302
(В) 2032
(Г) 2122
(Д) 2320

Задача №3
Буратино написал подряд 4 разные цифры, соблюдая условие, что каждая следующая цифра меньше предыдущей и общая сумма всех цифр равна 18. Второй была написана цифра 7. Какая цифра была написана третьей?
(A) 6
(Б) 5
(В) 4
(Г) 3
(Д) 2

Задача №4
В прямоугольнике 4х6, нарисованном на клетчатой бумаге, проведённая диагональ разрезает 8 клеточек. В прямоугольнике 4х8 — диагональ также разрезает 8 клеточек. А сколько клеточек разрежет диагональ, если её провести в прямоугольнике 4х7?
(A) 6
(Б) 7
(В) 8
(Г) 9
(Д) 10

Задача №5
В комнате сидят 10 человек одного из двух типов: одни лжецы, которые всегда лгут, другие рыцари, которые всегда говорят правду. Восемь из них сказали: “Хотя бы один из нас лжец”, остальные промолчали. Сколько может быть рыцарей среди присутствующих? (найдите все варианты и покажите, что нет других)
(A) 7 или меньше
(Б) 8 или 9
(В) 7 или 8
(Г) 9 или 10
(Д) 10 или больше

Задача №6
Сосчитайте, сколько всего треугольников изображено на рисунке? Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 3 класс
(A) 8
(Б) 10
(В) 12
(Г) 14
(Д) 16

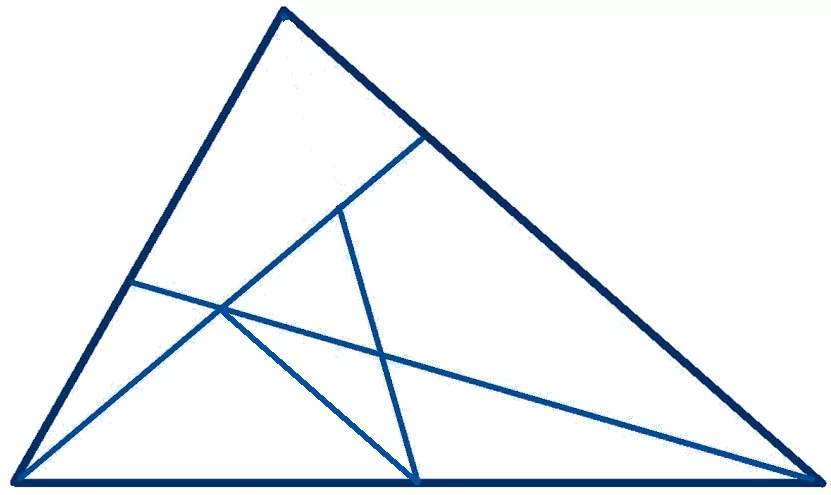
Задача №7
У Коли пятирублевых монет в три раза меньше, чем двухрублевых, а всего 33 рубля. Сколько монет у Коли?
(A) 7
(Б) 10
(В) 11
(Г) 12
(Д) 14

Задача №8
В банке лежали леденцы. Каждый из них с двумя вкусами: малина-яблоко, яблоко-груша или груша-малина. Известно, что леденцов с малиновым вкусом было 13, с яблочным – 9, а с грушевым – 8. Сколько леденцов надо достать из банки не глядя, чтобы среди них обязательно нашелся яблочно-малиновый?
(A) 10
(Б) 9
(В) 8
(Г) 7
(Д) 6

Задача №9
Какое самое меньшее значение может принимать сумма С + И + С + Т + Е + М + А + Т + И + К + А, если разным буквам соответствуют разные цифры, одинаковым – одинаковые, и чем меньше номер буквы в алфавите, тем меньшее число обозначает спрятанная за ней цифра?
(A) 22
(Б) 37
(В) 34
(Г) 25
(Д) 40

Задача №10
Электронные часы показывают 21:00 (см рисунок). Сколько маленьких огонёчков поменяет свечение, когда часы будут показывать 22:28?

(A) 12
(Б) 9
(В) 10
(Г) 13
(Д) 7

Задача №11
Костя умеет читать только буквы которые написаны правильно. Внутри автобуса висит объявление «СТОИМОСТЬ ПРОЕЗДА 25 РУБЛЕЙ». Сколько букв смог прочитать Костя, стоя на остановке напротив автобуса?
(A) 9
(Б) 8
(В) 12
(Г) 13
(Д) 10

Задача №12
В некотором месяце 5 пятниц. В этом месяце не может быть:
(А) 5 вторников
(Б) 5 сред
(В) 5 четвергов
(Г) 5 суббот
(Д) 5 воскресений

Задача №13
На какой из фигур на рисунке закрашена ровна одна треть треугольников?
Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 3 класс
(A) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5