Задания 1-го тура XIV олимпиады по математике для 4 класса
1-ый тур XIV олимпиады по математике прошел с 18 по 30 сентября 2023 года.
Задачи олимпиады
Задача №1
Мастеру нужно провести интернет из города до деревни Простоквашино. Расстояние между ними 20 километров. Чтобы протянуть провод, нужно поставить столбы через каждые десять метров. Сколько столбов понадобится? (А) 1999 (Б) 2002 (В) 2001 (Г) 2000
Гавва А. С.
Задача №2
К кормушке, которую повесила Оля, прилетают только воробьи и голуби. Воробушек съедает три семечки, а голубь – пять. Оля посчитала, что во вторник к ней прилетело 17 птиц и что они съели 71 семечку. Сколько воробушек прилетело к Оле во вторник? (А) 9 (Б) 8 (В) 7 (Г) 10
Гавва А. С.
Задача №3
Пираты считали сокровища. Старший из них заметил, что если каждый из пиратов добавит к имеющимся сокровищам по мешку золота, то всего мешков станет 42, а если, наоборот, каждый из пиратов заберёт по мешку, то мешков станет 28. А сколько мешков получит каждый из пиратов, если поровну разделить имеющиеся мешки с золотом между ними? (А) 6 (Б) 4 (В) 5 (Г) 10
Тодоров Е. И.
Задача №4
Некоторые кочки на болоте в лягушачьей деревне соединены мостиками, как показано на рисунке, лягушонок Прутик может перепрыгнуть с любой кочки на любую другую, но если между ними есть мостик, то лягушонок лучше пройдет по нему. Прутик вылез из болота на ближайшую кочку. Оттуда он за один “ход” (переход или “перепрыг”) добрался до кочки под номером 4 и от нее сделал еще один ход. Известно, что Прутик один раз перепрыгнул с кочки на кочку, и один раз прошел по мостику (но в каком порядке - неизвестно). Сколькими способами он мог это сделать? (А) 2 (Б) 4 (В) 6 (Г) 8
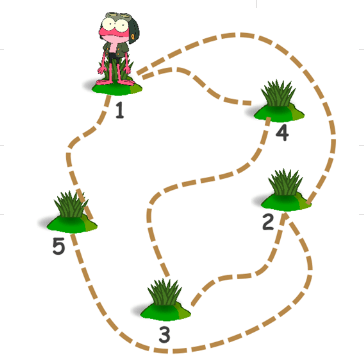
Галиулина В. Н.
Задача №5
В жилом комплексе “Кошачий” есть квартиры по одной, две и три комнаты, причём однокомнатных столько же, сколько и трёхкомнатных, а всего квартир ровно 300. Известно, что в двухкомнатных квартирах живёт по две кошки, в трёхкомнатных – по четыре, а в однокомнатных кошен нету. Сколько всего кошек живёт в жилом комплексе? (А) 300 (Б) 600 (В) 900 (Г) невозможно определить
Тодоров Е. И.
Задача №6
На стол выложены в алфавитном порядке карточки, на которых написаны буквы А, Б, В, Г, Д, Е, Ё, Ж, И и Й. На другой стороны каждой карточки написано целое число так, что сумма чисел на любых трёх подряд идущих карточках равна 16. Известно, что на другой стороне карточки в буквой А написано число 3, а на другой карточке с буквой И написано число 5. Какое число написано с другой стороны карточки с буквой Е? (А) 3 (Б) 8 (В) 5 (Г) 7
Тодоров Е. И.
Задача №7
В 7ы классе одной математической школы учится 28 человек. Когда строгий директор Александр Ильич спросил у Фёдора Фёдоровича Алексеева, сколько двоечников в 7ы, добрый Фёдор Фёдорович уклончиво ответил, что среди любых семи человек не менее трёх двоечников. Каково минимальное количество двоечников в 7ы? (А) 0 (Б) 28 (В) 14 (Г) 24
Тодоров Е. И.
Задача №8
В каждом узле паутины, выглядящей как сетка 8x8, сидит паук. Раз в минуту (начиная с 1-й) каждый паук переползает на соседний узел справа или снизу от него (если ползти некуда, он остается на месте). Какое количество пауков передвинутся со своего места когда наступит 9-я минута? (А) 0 (Б) 45 (В) 36 (Г) 28
Галиулина В. Н.
Задача №9
На каждой грани кубика написаны числа от 1 до 6. Сумма чисел на противоположных сторонах игрального кубика равна 7. Из восьми кубиков склеили один большой. Какая минимальная сумма чисел со всех его сторон могла получиться? (А) 48 (Б) 36 (В) 24 (Г) 72
Галиулина В. Н.
Задача №10
Гарри Поттер и его друзья – Рон, Гермиона и Невилл играют в волшебную дженгу. Они по очереди достают дощечки из башни и кладут их наверх. Дощечки с самого верхнего слоя брать нельзя. В начале игры башня всего четыре слоя в высоту. Упадет она лишь тогда, когда в каком-нибудь слое совсем не останется дощечек. Кто проиграет при правильной игре (т.е все игроки делают наилучшие возможные ходы), если первым ходит Гарри, вторым – Рон, третьей – Гермиона, четвертым – Невилл? (А) Гарри (Б) Рон (В) Гермиона (Г) Невилл

Галиулина В. Н.
Задача №11
В журнале «Суперкиборги» есть 4 выпуска. К первому выпуску прилагаются голова и туловище робота, ко второму – туловище, руки и ноги, к третьему – руки и голова, к четвертому – голова и ноги. Какое наименьшее количество журналов нужно купить Денису, если он хочет собрать армию из десяти таких роботов? (А) 17 (Б) 18 (В) 19 (Г) 20
Галиулина В. Н.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Ответ | В | В | В | Г | Б | В | Г | В | В | B | А |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


