Пробная олимпиада

Пройдите пробную олимпиаду по математике для 1–9 классов.
IV олимпиада по математике прошла 27 января 2019 года.
Задача №1
Дед Мороз собирает сладкий подарок. В коробочку он может насыпать рафаэлки, мармеладки и шоколадные конфетки. Всего в подарке должно оказаться 15 конфет. Сейчас у него осталось 14 шоколадных конфет, 5 рафаэлок и 7 мармеладок. Сколькими способами Дед Мороз может собрать последний подарок?
Задача №2
На доске 11х11 Ника закрасила несколько прямоугольников 1х3 по линиям сетки. Оксана заметила, что не может из этой доски вырезать квадрат 3х3 без закрашенной клетки. Какое наименьшее количество прямоугольников могла закрасить Ника? Покажите, как Ника закрасила прямоугольники и объясните, почему это количество самое маленькое.
Задача №3
Разделите фигуру на 4 равные части, чтобы в каждой был круг и ромб.
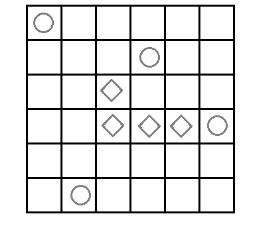
Задача №4
В мешке есть буквы К, Р, О, Т. Всего 26 карточек. Сколько каждого вида, неизвестно. Букв К меньше, чем букв Р. Букв Р меньше чем букв О. Букв О меньше чем букв Т. Буквы достают по одной из мешка, не глядя. Чтобы точно собрать слово КРОТ, нужно вытащить 22 карточки. Чтобы собрать слово РОТ нужно вытащить 21 карточку. Чтобы собрать набор КРТ , нужно вытащить 20 карточек. Сколько карточек каждого вида в мешке?
Задача №5
На День Дружбы девочки дарили мальчикам открытки, а мальчики дарили девочкам наклейки. В классе 25 человек. Никто не получил два подарка от одного и того же человека. Всего было сделано 300 подарков. Сколько в классе может быть мальчиков, а сколько девочек?
Задача №6
Можно ли из всех цифр, взятых по одному разу, составить два числа, чтобы одно нацело делилось на другое. И оба числа имели больше чем один разряд. Все цифры должны быть использованы.
Ответы на задачи №1-6 в формате разборов
1-й тур: 23 сентября — 6 октября
2-й тур: 27 октября
Олимпиада по математике
ШЕСТНАДЦАТАЯ МЕЖДУНАРОДНАЯ ОЛИМПИАДА СИСТЕМАТИКИ
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Зарегистрироваться
Бесплатно



