Задания IX олимпиады по математике для 6 класса

Назовем число красивым, если его сумма цифр делится на 3 без остатка. Существует ли два подряд идущих красивых числа?

Придумайте наибольшее натуральное число, меньшее миллиона, все слова при записи которого по-русски, начинаются на одну и ту же букву.

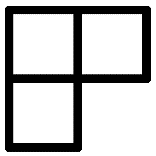
От шахматной доски Петя отпилил поле С3, а Вася поле Е8. Докажите, что у Васи больше способов замостить доску трехклеточными уголками без дыр и наложений.

Есть мешок монет, каждая из которых весит 3 или 4 грамма. Монеты можно взвешивать на чашечных весах, но в момент взвешивания на одну из чаш прыгает невидимый гном весом в 1 грамм. Как сделав не более трех взвешиваний поймать гнома (указать на чашу, где он в данный момент находится)?

На острове живут рыцари и лжецы. Рыцари всегда говорят только правду, лжецы – всегда лгут. 16 шариков, 12 из которых белые и 4 черные, раздали поровну 4 островитянам. Каждый из них про свой набор шариков высказал одно утверждение:
"Черных больше, чем белых",
"Черных не меньше, чем белых",
"Черных и белых поровну",
"Белых не более одного".
Какое наибольшее число рыцарей могло быть среди них?

Маша умеет выговаривать все буквы, кроме М и Ш. Сколько чисел от 1 до 1000 сможет правильно произнести Маша?

У Васи есть карточки с числами 3, 4, 6, 8, 12, 20, 28. Вася хочет разложить карточки в две кучки так, чтобы суммы чисел на карточках в кучках были равны (а количество карточек может различаться). Возможно, какие-то карточки придется выкинуть. Вася старается выкинуть как можно меньше карточек. Сколько он выкинул? Объясните, почему нельзя выкинуть меньше карточек. Покажите, как можно поделить карточки на две кучки.

Можно ли расставить числа от 1 до 20 в таблице 9х11 (числа могут повторяться) так, для каждой пары чисел нашлось место в таблице, где они занимают соседние по стороне клетки?

Серёжа собирает игрушечные железные дороги. У него есть несколько наборов, в каждом из которых разное количество вагонов. Он заметил, что если все наборы объединить в один состав, то в нем будет 121 вагонов. Если взять три самых маленьких набора, то в них будет 28 вагонов, а в трех самых больших — 53 вагона. Когда Серёжа поделился этим фактом с другом Вовой, тот подумал и сказал, что точно знает несколько наборов, которые есть у Серёжи и назвал сумму вагонов в них. Восстановите вычисления Вовы и сообщите эту сумму вагонов в наборах, которые можно однозначно определить.