Задания III олимпиады по математике для 3-4 классов

В мешке лежат фигуры: круглые и квадратные, красные и синие. Ника достала 4 разные фигуры и выложила их в ряд так, чтобы цвета чередовались. Докажите, что в этом ряду рядом лежат две фигуры одинаковой формы.

Раздели фигуру по линиям «сетки» на три равные по форме и размеру части.

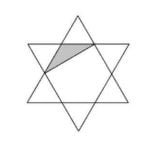
Площадь закрашенного треугольника равна 1. Найдите площадь всей звезды. Шестиугольник правильный, «лучи» звезды — равносторонние треугольники.

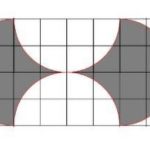
Найдите площадь (в клетках) всей серой области.

В мешке лежат 12 конфет: шоколадные, мармеладные и мармеладно-шоколадные. Известно, что среди любых 5 конфет найдётся та, в которой есть мармелад. Среди любых 6 конфет найдётся та, в которой есть шоколад. Какое наименьшее число мармеладно-шоколадных конфет может быть в мешке?

Расставьте на поле 4х4 ферзя, слона, коня, ладью и короля так, чтобы они не били друг друга.