Задания 1-го тура XVII олимпиады по математике для 8 класса
1 тур XVII олимпиады по математике прошел с 21 января по 9 февраля 2025 г.
Задачи олимпиады
Задача №1
В некоторый бассейн, заполненный до краев, который имеет форму параллелепипеда, поместили слона, целиком — вплоть до ушей и хобота (слон при этом не задохнулся, так как был в специальной маске). В результате в бассейне стало на 20% воды меньше, чем было в начале. Поместив в бассейн второго слона, объем жидкости снизился уже на 15%, относительно последнего показателя. Третий же слон, помещенный в бассейн, снизил уровень воды на 5%, четвертый на 4%, пятый на 1%. Каков объем оставшейся в бассейне воды, если среднестатистический “объем” слона – 3 кубических метра (ответ округлить до десятых).
А) 5.7 Б) 7.5 В) 9.2 Г) 13.1 Д) 23.9
Миронов Д. Р.
Задача №2
Четырехугольник ABCD с равными диагоналями вписали в квадрат EFGH так, что вершины A, B, C, D оказались на сторонах EF, FG, GH и HE соответственно. Найдите отношение площадей четырехугольника и квадрата, если FB:FG = 1:8, FB:DH = 1:3
А) 1/2 Б) 4/7 В) 5/8 Г) 2/3
Галиулина В. Н.
Задача №3
Известно, что 5/4 * 6/5 * 7/6 * 8/7 * ... * x/y = 5. Чему равна сумма натуральных чисел x и y?
А) 11 Б) 37 В) 39 Г) 41
Тодоров Е. И.
Задача №4
Числа х, у и z имеют следующий вид. Чему равно произведение x⋅y⋅z?
А) 12 Б) 6 В) 8 Г) 18

Миронов Д. Р.
Задача №5
В треугольнике ABC сторона AB = 13, AC = 5, BC = 12. На стороне AB отмечена точка D таким образом, что периметры треугольников ACD и BCD оказались равны. Чему равна площадь треугольника ACD?
А) 15/2 Б) 90/13 В) 20 Г) 300/13 Д) 30
Тодоров Е. И.
Задача №6
Про действительные числа x, y и z известно, что x*y*z<0 Какие значения принимает выражение?
А) -1, 0 и 1 Б) -2 и 2 В) -2, 0 и 2 Г) -1, 0, 1 и 2 Д) -2, -1, 0, 1 и 2
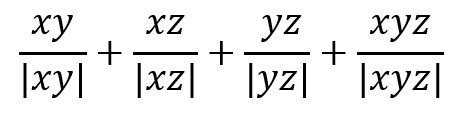
Тодоров Е. И.
Задача №7
Федя взял все чётные числа от 1 до 1000, вычеркнул все, которые делились на 5, а остальные перемножил. Какова последняя цифра результата, полученного Федей?
А) 2 Б) 4 В) 6 Г) 8
Тодоров Е. И.
Задача №8
Для проведения соревнований по бегу на стадионе есть 6 дорожек, то есть одновременно в забеге может принимать участие до 6 бегунов. К сожалению, судьи потеряли таймер, поэтому не засекают время, а просто пропускают в следующий этап только бегуна, прибежавшего первым в данной шестёрке (для удобства будем считать, что двоих победителей ни в каком забеге быть не может). На каждый забег отводится по 10 минут. Кроме того, известно, что между своими забегами спортсмен обязательно должен отдыхать тоже хотя бы 10 минут. Через какое минимальное время после начала соревнований будет известен победитель, если всего в соревновании участвует 216 бегунов?
А) 6 часов Б) 7 часов 10 минут В) 7 часов 20 минут Г) 7 часов 30 минут
Тодоров Е. И.
Задача №9
Петя и Вася играют в игру. Изначально на доске написано число s. За один ход разрешается к написанному на доске числу прибавить 20 или умножить его на 25, старое число стереть и вместо него написать результат своих вычислений. Побеждает тот, после чьего хода на доске впервые окажется число 2025 или больше. Первым ходит Петя. При каком наибольшем s Петя не сможет выиграть за один ход, но точно выиграет за два?
А) 3 Б) 60 В) 61 Г) 81
Тодоров Е. И.
Задача №10
Ленивец Глеб каждый день пробегает целое количество километров, готовясь к соревнованиям ровно по часу в день. Четыре дня подряд Глеб старался бегать всё быстрее и быстрее, для этого он каждый день бежал с такой постоянной скоростью, что на преодоление каждого километра ему требовалось некоторое целое количество минут. Будем называть это количество минут темпом бега Глеба. Оказалось, что темп Глеба каждый день уменьшался на одинаковое количество минут, большее 1. Сколько километров пробежал Глеб за эти четыре дня подготовок?
А) 25 Б) 26 В) 31 Г) 35 Д) 59
Тодоров Е. И.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Д | В | В | А | Б | Б | В | В | Б | А |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


