Задания 1-го тура XVII олимпиады по математике для 9 класса
1 тур XVII олимпиады по математике прошел с 21 января по 9 февраля 2025 г.
Задачи олимпиады
Задача №1
Во дворце Чудовища каждая дверь ведёт из одной комнаты в другую. Красавица заметила, что, если закрыть не более чем 1/d (для некого целого d) всех дверей (двери можно выбирать любые!), то из любой комнаты всё ещё можно будет попасть в любую другую. Какое наибольшее количество комнат может быть во дворце?
А) d Б) 2d-1 В) 2d Г) Сколь угодно много
Галиулина В. Н.
Задача №2
Четырехугольник ABCD с равными диагоналями вписали в квадрат EFGH так, что вершины A, B, C, D оказались на сторонах EF, FG, GH и HE соответственно. Найдите отношение площадей четырехугольника и квадрата, если FB:FG = 1:8, FB:DH = 1:3
А) 1/2 Б) 4/7 В) 5/8 Г) 2/3
Галиулина В. Н.
Задача №3
Найдите максимальное значение числа n, при котором значение выражения 48!+49!+50! нацело делится на 5 n.
А) 12 Б) 13 В) 14 Г) 16 Д) 18
Тодоров Е. И.
Задача №4
Числа х, у и z имеют следующий вид. Чему равно произведение x⋅y⋅z?
А) 12 Б) 6 В) 8 Г) 18

Миронов Д. Р.
Задача №5
Ни одно из действительных чисел x, y и z не равно нулю. Какие значения принимает выражение?
А) -1, 0 и 1 Б) -1 и 7 В) -7 и 1 Г) -7 и 7 Д) -7, -1, 0, 1 и 7
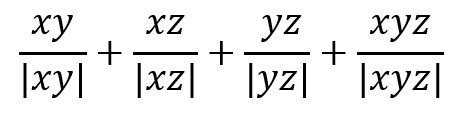
Тодоров Е. И.
Задача №6
Полуокружность касается стороны AB треугольника ABC со сторонами AB=5, AC=4, BC=3 (см. рисунок). Найдите её радиус.
А) 2/3 Б) 3/2 В) sqrt(3)/2 Г) 3/4 Д) 3
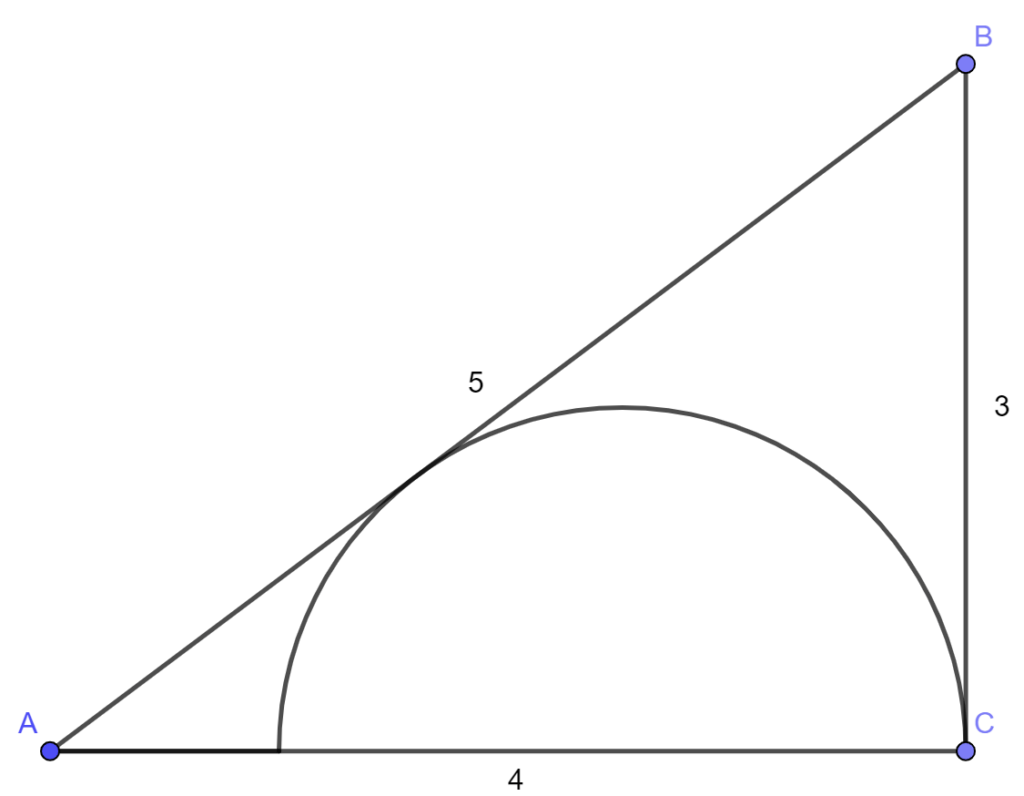
Тодоров Е. И.
Задача №7
Число x является решением данного уравнения: 3(3x) = 333 Какое из утверждений верно для значения x?
А) 0 < x < 1 Б) 1 < x < 2 В) 2 < x < 3 Г) 3 < x < 4
Миронов Д. Р.
Задача №8
В Зверином королевстве проходят соревнования по бегу. Ленивец Глеб каждый день пробегает целое количество километров, готовясь к соревнованиям ровно по часу в день. Четыре дня подряд Глеб старался бегать всё быстрее и быстрее, для этого он каждый день бежал с такой постоянной скоростью, что на преодоление каждого километра ему требовалось некоторое целое количество минут. Будем называть это количество минут темпом бега Глеба. Оказалось, что темп Глеба каждый день уменьшался на одинаковое количество минут, большее 1. Сколько километров пробежал Глеб за эти три дня подготовок?
А) 25 Б) 26 В) 31 Г) 35 Д) 59
Тодоров Е. И.
Задача №9
Петя и Вася играют в игру. Изначально на доске написано число s. За один ход разрешается к написанному на доске числу прибавить 20 или умножить его на 25, старое число стереть и вместо него написать результат своих вычислений. Побеждает тот, после чьего хода на доске впервые окажется число 2025 или больше. Первым ходит Петя. При каком наибольшем s Петя не сможет выиграть за один ход, но точно выиграет за два?
А) 3 Б) 60 В) 61 Г) 81
Тодоров Е. И.
Задача №10
Пусть функция f от натурального числа a возвращает сумму квадратов цифр этого числа. Например, f(47) = 42 + 72 = 65. Из всех чисел a, все цифры в которых различны и не равны нулю, для которых f(a)=41, выбрали наибольшее. Чему равно произведение его цифр?
А) 12 Б) 18 В) 20 Г) 24
Тодоров Е. И.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Б | В | В | А | Б | Г | Б | А | Б | Б |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


