Задания 2-го тура XVI олимпиады по математике для 9 класса
2 тур XVI олимпиады по математике прошел 27 октября 2024 года
Задачи олимпиады
Задача №1
В остроугольном треугольнике ABC на стороне AC отметили точку M и провели из нее перпендикуляры MN и MP к сторонам AB и BC соответственно. Из точки C провели высоту CH. На стороне AC отметили такую точку D, что ∠HCA = 2∠AHD. Оказалось, что DC = MN + MP. Доказать, что треугольник ABC равнобедренный
Галиулина В. Н.
Задача №2
Шестизначное число заканчивается на цифру 7, а если эту цифру переставить с последнего места на первое, число увеличится в 4 раза. Чему было равно изначальное число?
Тодоров Е. И.
Задача №3
На рисунке изображён квадрат ABCD. Точки E, F, G, H являются серединами сторон квадрата. Внутри трёх четырёхугольников указана их площадь. Найдите диагональ исходного квадрата. В ответе укажите квадрат этого числа.
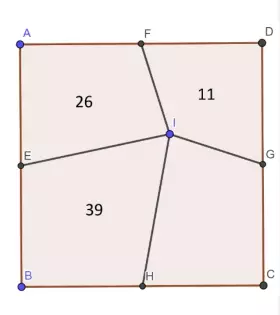
Миронов Д. Р.
Задача №4
Круг разбит на 8 одинаковых секторов. Будем называть маленьким кусочек, равный одному сектору круга (с углом 45°), а большим - кусочек, равный двум склеенным секторам круга (с углом 90°). Замощением называется способ положить большие и маленькие кусочки на круг так, чтобы края кусочков совпадали с линиями разреза на круге, а сами кусочки покрывали круг целиком и в один слой. Если два замощения можно совместить поворотом, мы всё равно будем считать их различными. Сколько различных замощений круга существует?
Тодоров Е. И.
Задача №5
Начинающие грузчики Ваня и Женя сложили три кубических ящика в кузов машины, как получилось (как именно получилось -смотрите на рисунке), причём угол маленького ящика лежит ровно на углах больших ящиков. Известно, что объём нижних ящиков одинаковый, а объём верхнего - в два раза меньше. Чтобы верхний ящик не упал в пути, Ваня и Женя привязали его углы к углам нижних ящиков верёвками, как показано на рисунке. Известно, что длина верёвки BG равна 256 сантиметров. Чему равна длина верёвки IE?
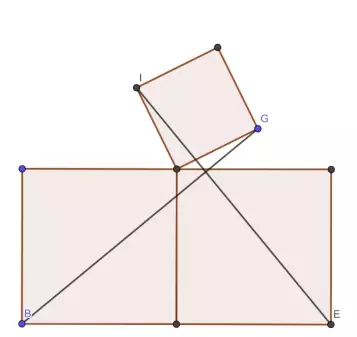
Тодоров Е. И.
Задача №6
Хоккеист Никита запустил шайбу из левого нижнего угла прямоугольного поля. Шайба прилетела в правый борт, отскочила от него, ударилась о верхний борт, потом ударилась о левый борт, и, наконец, прилетела точно в правый нижний угол. Известно, что при каждом отскоке шайба отлетала от борта под тем же углом, под которым прилетела в него. Длина нижнего борта поля равна 15 метров, а общее расстояние, которое пролетела шайба, равно 51 метр. Чему равна длина правого борта поля?

Тодоров Е. И.
Задача №7
В прошлом году математику Джону раз в месяц снилось некоторое натуральное число, причём каждый раз новое. В новогоднюю ночь Джон записал все двенадцать приснившихся ему чисел на листе бумаги. Верно ли, что среди них всегда можно выбрать четыре различных числа a, b, c и d так, чтобы произведение (a-b)*(c-d) делилось на 99?
Тодоров Е. И.
Задача №8
В строку в порядке возрастания выписаны двадцать ненулевых чисел, из которых ровно p положительных. Число a стоит на шестом месте, считая от начала строки. Затем все числа заменили на обратные по умножению к ним (то есть каждое x заменили на 1/x), и полученный список из 20 чисел вновь упорядочили по возрастанию. На каком месте оказалось число 1/a?
Тодоров Е. И.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



