Задания 2-го тура XVII олимпиады по математике для 3 класса

В семье четверо детей. Возраст Алекса равен сумме возрастов Бори и Кати. Четыре года назад возраст Дани был равен сумме возрастов Бори и Кати. Восемь лет назад возраст Алекса был вдвое больше возраста Дани. Кто из детей самый старший? Ответ объясните.

На рисунке «H» образована путем удаления двух прямоугольников 2 x 4 из прямоугольника 6 x 10. «H» необходимо полностью выложить плитками 1 x 1, которые поставляются в коробках по 6 штук. Какое наименьшее количество коробок с плиткой необходимо купить, чтобы выложить «H»?

Кот Мур-Мяу живет в Англии и каждый час слышит звон Биг-Бена. У него есть ненастроенные часы, минутная стрелка которых каждый час проворачивается на полный круг и еще 18 минут. Мур-Мяу знает, что вчера в полночь его часы показывали правильное время. Что будут показывать часы котика сегодня в полночь?

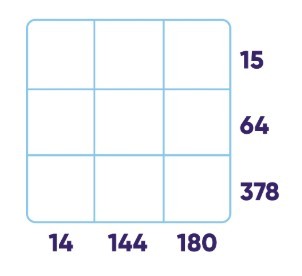
В квадрат 3х3 расставили числа от 1 до 9, без повторений. Числа справа — это произведения чисел в соответствующих строках, а числа снизу — произведения чисел в соответствующих столбцах. Найдите сумму чисел, стоящих в углах квадрата.

PIN-код Ники — это 4-значное число. Сумма его цифр равна 22. Если читать слева направо, то вторая и третья цифры одинаковы. Вторая цифра в два раза больше четвертой. Первая цифра в четыре раза меньше третьей. Какой же у Ники PIN-код?

Саша и Петя договорились сначала порезать тортик, и только потом его есть. Саша разрезал торт пополам и половину отдал Пете. Петя отрезал от своей половины по кусочку пока не сделал 111 разрезов. Саша разрезал свою половину на 3 части, потом каждую часть тоже на 3 части и продолжил резать так дальше. Могло ли в итоге получиться 2024 кусочка?

Сейчас счетчик мандаринов, съеденных Павликом показывает 45125. В этом числе цифра 5 встречается дважды. Какое минимальное количество мандаринов нужно съесть Павлику, чтобы на его счетчике вновь оказались две одинаковые цифры?

Миша загадал двузначное число, про которое известны следующие факты: – при делении на 6 оно даёт остаток 3 – при делении на 7 оно даёт остаток 4 – число не является точным квадратом (то есть его нельзя получить, умножив друг на друга два одинаковых натуральных числа) Какой остаток это число даёт при делении на 19?