Задания 2-го тура XVII олимпиады по математике для 8 класса
2 тур XVII олимпиады по математике прошел 2 марта 2025 г.
Задачи олимпиады
Задача №1
Дан стеклянный параллелепипед, со сторонами a*b*8 (a≠b≠c a,b,c >1) состоящий из стеклянных, единичных кубиков. На сторонах граней размещаются излучатели 3-х цветов, параллельные сами себе и одной из граней. Притом все излучатели одного цвета ориентированы одинаково и не совпадают с другими цветами (все единичные кубики освещены одним цветом строго с 1 стороны). После включения оказалось, что кубиков, освещаемых красным цветом — 45, синим — 72, зелёным — 72. Синих излучателей потребовалось больше, чем зелёных и красных вместе взятых, а красных и зелёных поровну. Одноцветных кубиков не было совсем. Разноцветных кубиков оказалось: красно-синих — 27; зелёно-красных — 30; сине-зелёных — 41; трёхцветных — 16. Вопросы: а) Восстановите размер параллелепипеда б) Каким граням (укажите их размеры) перпендикулярны какие излучатели в) Сколько кубиков не пронзают лучи?
Иванюк Д. В.
Задача №2
Известно, что для цифр x1, x2, x3 и x4 выполняется условие x1+x2≤9 и x3+x4≤9. А d — это некоторое натуральное число. Сколько решений имеет уравнение:
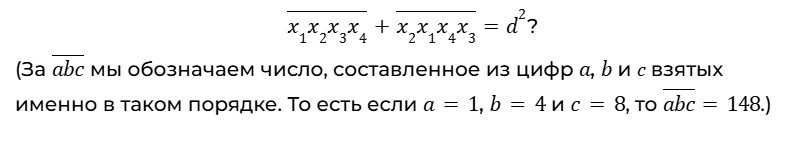
Галиулина В. Н.
Задача №3
Три полуокружности пересекаются и образуют угол zxy равный 30 градусам. Площадь каждой полуокружности 24, х y z центры недорисованных окружностей. Найдите суммарную площадь заштрихованной части.
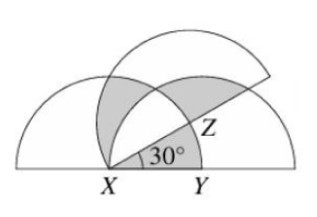
Миронов Д. Р.
Задача №4
Найдите все пары натуральных чисел x и y, являющихся решениями уравнения xy + 4y - 7x = 47
Тодоров Е. И.
Задача №5
Лиза нарисовала на клетчатом поле красную фигурку (см. рисунок). Какое минимальное количество клеточек Лиза должна добавить к своей фигурке, чтобы её можно было разрезать на S-тетрамино (так называются фигурки, нарисованные синим справа)?
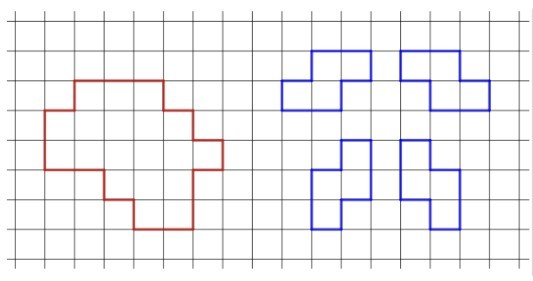
Тодоров Е. И.
Задача №6
На плоскости отмечено 15 синих точек и 65 красных. Некоторые точки соединены отрезками. Оказалось, что если две точки не соединены отрезком, то найдется красная точка, которая соединена отрезками с каждой из них. Докажите, что есть точка, соединенная отрезком как минимум с девятью другими.
Галиулина В. Н.
Задача №7
Арифметическая прогрессия — это последовательность чисел, в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему некоторого постоянного числа, которое называется шагом прогрессии. Например, наборы чисел 1, 2, 3, 4, 5, ... и 2, 5, 8, 11, 14, ... — это арифметические прогрессии с шагами 1 и 3 соответственно. Известно, что числа в любой строке и любом столбце в таблице ниже составляют арифметическую прогрессию. Чему равно число в центре таблицы?

Тодоров Е. И.
Задача №8
На рисунке изображен прямоугольник AEFJ внутри правильного десятиугольника ABCDEFGHIJ. Найдите отношение площади прямоугольника к площади десятиугольника
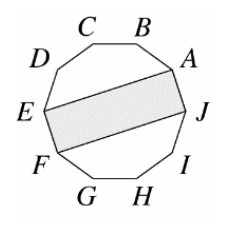
Галиулина В. Н.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



