Задания 1-го тура XVIII олимпиады по математике для 8 класса
1 тур XVIII олимпиады по математике прошел с 16 по 29 июня 2025 г.
Задачи олимпиады
Задача №1
Двое мудрецов загадали по числу от 1 до 100. Сначала первый мудрец сказал: “Если твоё число делится на моё, то я буду знать, чему равно твоё число”. На что второй мудрец сказал: “Твоё число точно делится на моё”. Чему равно произведение загаданных мудрецами чисел, если их сумма равна 100?
А) Нельзя однозначно определить Б) 99 В) 900 Г) 1875
Галиулина В.Н.
Задача №2
На картинке все треугольники с черными сторонами правильные и картинка симметрична относительно всех трёх красных осей. Площадь всей фигуры равна 1. Площадь серой части равна 0,75. Чему равна площадь маленькой белой звезды в центре?
А) 1/16 Б) 1/28 В) 1/32 Г) 1/64
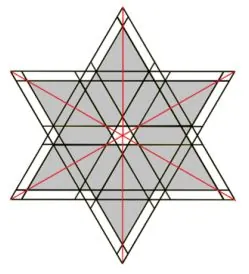
Манжина О.А.
Задача №3
Выберите верное (ые) утверждение(я): 1. Отношение длины окружности к диаметру этой окружности зависит от радиуса данной окружности. 2. Равносторонние треугольники являются также и равнобедренными, однако, в обратную сторону это правило не работает. 3. Есть два куба: первый имеет размеры 9х9х9 см, второй точно такой же, но с вырезанным кубиком 1х1х1 см в центре фигуры. Если задаться целью их покрасить, то на первый куб уйдет больше краски. 4. Чисел, которые будут записываться бесконечно долго, и при этом не превышают ноль — не существует.
А) 1,2,4 Б) 2,3 В) 2 Г) 1
Миронов Д.Р.
Задача №4
За один день в Систематике проходит 8 групповых уроков длительностью 1 час (перерыв между соседними уроками 6 минут). Вася набрался сил, и чтобы вспомнить забытое за лето, решил посетить все уроки разом. Однако, уже после пяти минут он растерял мотивацию, и начал смотреть на настенные часы, наблюдая за тем, как же медленно двигается часовая стрелка. Какой же угол (в градусах) описала часовая стрелка за всё время проведения занятий, с учетом перерывов?
А) 100° Б) 140° В) 130. 5° Г) 150. 8° Д) 261°
Миронов Д.Р.
Задача №5
Окружность касается гипотенузы и катета прямоугольного треугольника и делит другой катет на отрезки длины 6, 18 и 32, считая от вершины прямого угла. Чему равна гипотенуза?
А) 56 Б) 60 В) 64 Г) 70 Д) 72
Евдокимов М.А.
Задача №6

Галиулина В.Н.
Задача №7
Сколько существует пар натуральных чисел n, m m таких, что n+(n+1)+(n+2)+… +(n+m)=1000?
А) 2 Б) 3 В) 4 Г) 5
Галиулина В.Н.
Задача №8
Сколько решений в натуральных числах имеет уравнение 8a=3ab−12b?
А) 0 Б) 1 В) 2 Г) 3 Д) бесконечно много
Галиулина В.Н.
Задача №9
Отношение двух положительных чисел равно отношению их суммы к их разности. Каково это отношение?

Миронов Д.Р.
Задача №10
Петя выписывает на доску числа. Первые три числа — это 2, 3 и 5. Каждое следующее число равно сумме всех предыдущих минус их количество. Например, на четвёртом месте будет стоять (2 + 3 + 5) − 3 = 7, на пятом – (2 + 3 + 5 + 7) − 4 = 13 и так далее. Чему равна сумма членов этой последовательности с чётными номерами, не превосходящими 20 (то есть сумма второго, четвёртого, шестого, … и двадцатого членов последовательности)?

Тодоров Е.И, Галиулина В.Н.
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Б | Г | В | Д | Г | В | Б | В | Г | Г |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


