Задания Тринадцатой Олимпиады по математике Весна 2023 1 тур 6 класс

1 тур олимпиады по математике прошёл с 15 мая по 7 июня 2023 года

Задача №1
Согласно данным из открытых источников, максимальная скорость Сапсана (птица) составляет 108 м/с, а скорость «самого быстрого электромобиля» Tesla Model S Plaid составляет 320 км/ч. Кто и во сколько раз быстрее?
(А) Скорость одинаковая
(Б) Птица быстрее в ≈3 раза
(В) Птица быстрее в ≈1,2 раза
(Г) Машина быстрее в ≈3 раза
(Д) Машина быстрее в ≈1,2 раза

Задача №2
Снята с конкурса

Задача №3
Из куба 3х3х3 вырезали несколько кубиков как показано на рисунке.
Как изменилась площадь поверхности? (вырез идёт по кругу)

(А) Увеличилась на 9
(Б) Увеличилась на 8
(В) Увеличилась на 7
(Г) Уменьшилась на 7
(Д) Не изменилась

Задача №4
Учитель загадал детям число, состоящее из цифр от 1 до 4 (цифры могут повторяться), и попросил ребят сделать предположение о загаданном числе. За каждую цифру, стоящую на правильном месте, он ставил галочку. Какое число загадал учитель? Введите его.

Задача №5
Сколько решений есть у уравнения:

(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4

Задача №6
У вас есть набор палочек, лежащих в виде сетки. Вы забираете палочки по одной начиная с самого верха. Чему будет равно значение полученного выражения? Пожалуйста, не забывайте про порядок действий. В ответ введите число.

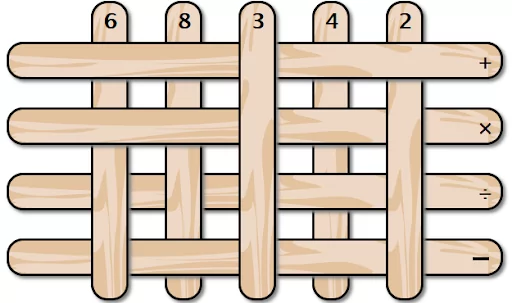
Задача №7
Бельчонок Натти просто обожает сладости. Он купил в лавке несколько бутылок вишневого сиропа и, недолго думая, выпил их все. В той же лавке можно обменять некоторое количество (одно и то же) пустых бутылок на целую бутылку сиропа. Бельчонок возвращался в лавку несколько раз чтобы совершить обмен, и, в конечном итоге, у него осталось 5 пустых бутылок. Какое количество бутылок могло быть у Натти изначально, если он получил еще 6 бутылок сиропа путем обмена?
(А) 29
(Б) 31
(В) 33
(Г) 34
(Д) 35

Задача №8
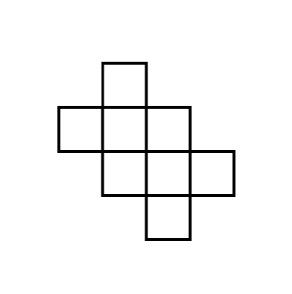
Сколько прямоугольников в фигуре на картинке?

(А) 8
(Б) 13
(В) 20
(Г) 21
(Д) 24

Задача №9
Команды зайчиков и ёжиков соревновались в эстафете. Каждый участник добегал до белой линии и возвращался обратно, после чего передавал эстафету следующему товарищу по команде. Ёжик Пых, у которого был номер 5, встретил зайчика Прыга с тем же номером на расстоянии в 2/5 пути до белой линии, когда тот уже возвращался обратно. Сколько было участников в одной команде, если последний зайчик и предпоследний ёжик финишировали одновременно? Участники одной команды бегают с одинаковой скоростью.
(А) 8
(Б) 10
(В) 11
(Г) 13
(Д) Невозможно определить

Задача №10
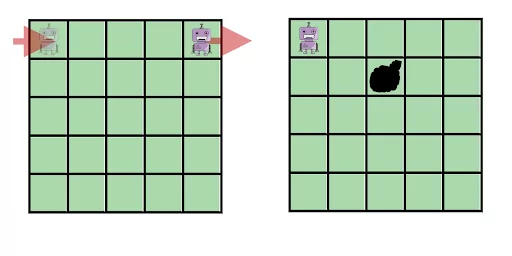
Слепой робот-уборщик может передвигаться по полю 5×5 только вниз и вправо. Как только он выходит за пределы поля он мгновенно материализуется на другой стороне поля (как показано на рисунке, за один шаг робот переместится из крайней правой клетки в крайнюю левую). В указанной клетке лежит куча мусора. Поскольку робот не может ее видеть, он действует так: сначала делает 13 шагов вправо, потом 11 шагов вниз и повторяет эти действия до тех пор, пока куча не будет найдена. Через сколько ходов поле станет чистым? Робот стартует из левой верхней клетки.

(А) 3
(Б) 14
(В) 28
(Г) 66
(Д) Никогда